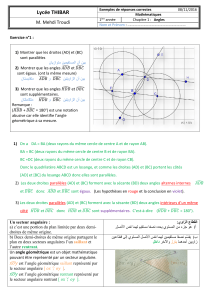
Éléments de base de géométrie

•
P
B
A
(d)
(AB)
(d)
A(d)A(d)A∈(d)

C(d)C(d)
C6∈ (d)
O
C
[OC)
•[
•)
→
[AB] (AB)A B
A B [AB]
N
A
I
B
I[AB]AI =IB
→
→

B
A
O
C
t
x
\
AOB
\
BOA
[
AOC
d
xOt
x t
→
→
90◦

180◦
0◦90◦
90◦180◦
→
→
O
y
x
z
d
xOy
d
yOz
x
z
y
O
(Oy)
d
xOz
→
→

(d1)⊥(d2)
→
→
(d1) (d2) (d) (d1)
(d2)
(d1)//(d2)
→
→
→