énoncé

Devoir sur feuille 3 : premier concours blanc
le jeudi 8 janvier 2015
Question : On désigne par n un nombre entier strictement supérieur à 1.
Un sac contient des boules rouges et des boules blanches, indiscernables si ce n’est par la couleur. La proportion
de boules rouges est p, où 0 < p < 1 ; celle des boules blanches est q = 1 − p. On effectue une suite de tirages
d’une boule, avec remise de la boule tirée après chaque tirage, selon la règle suivante :
– dès qu’une boule rouge est tirée, on arrête les tirages ;
– si les n premières boules tirées sont blanches, on arrête les tirages.
1. Déterminer le nombre maximal de tirages que l’on effectue lors de cette expérience.
2. On introduit pour tout k ∈ [[1, n]] l’événement Ak ”l’expérience s’achève au bout de k tirages”.
a) Introduire des événements qui permettent de décrire l’expérience.
b) Décrire les événements Ak à l’aide de ces événements (on pensera à distinguer le cas k = n).
n
P
P (Ak ) = 1.
c) en déduire pour tout k ∈ [[1, n]], P (Ak ), puis vérifier que
k=1
Exercice 1: inspiré de Eslsca 95


0 0 0
On considère la matrice D = 0 3 0 et l’ensemble E = {M ∈ M3 (R) / M D = DM }.
0 0 3
1. Montrer que E ainsi écrit est un sous-espace vectoriel de M3 (R)
2. Déterminer les matrices de E.
3. Trouver alors une base de E.
4. On considère l’équation M 2 − M + D = 0 d’inconnue M ∈ M3 (R).
(a) Montrer qu’il n’existe pas de solutions M telles que M soit diagonale.
(b) Montrer que si M est solution, alors M ∈ E.
(c) Montrer qu’il existe une infinité de solutions à cette équation.
Exercice 2: inspiré d’hec E 2003 et d’eml S 99
ln(1−x)
− x
si x 6= 0
Soit f la fonction définie par f (x) =
1
si x = 0
1. Déterminer l’ensemble de définition de f , que l’on notera D.
2. f se prolonge-t-elle par continuité en 1 ?
3. Etudier la limite de f en −∞. Interpréter.
4. Montrer que f est continue sur D.
5. Montrer que f est dérivable sur D. On pourra admettre la limite suivante :
ln(1+x)−x
−→
x2
x→0
− 12 .
6. Calculer f 0 (x) pour tout x 6= 0.
7. On pose pour tout t ∈] − ∞, 1[, g(t) =
t
1−t
+ ln(1 − t). Déterminer le signe de g.
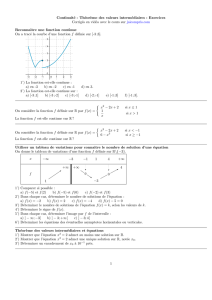
8. Dresser le tableau de variations de f .
9. Dessiner la courbe de f , en précisant les asymptotes et la tangente à l’origine.
Exercice 3: Esclsca 90
On considère l’ensemble S des matrices de la forme P =
a
b
avec (a, b) ∈]0, 1[×]0, 1[.
1−a 1−b
Partie I :
1. L’ensemble S est-il un sous-espace vectoriel de M2 (R) ?
a
b
2. Soit a, b ∈]0, 1[ et P =
∈ S.
1−a 1−b
Montrer que P 2 = (1 + d)P − dI2 où d = a − b et I2 est la matrice identité de M2 (R).
3. Montrer alors que : ∀n > 1,
Pn =
1 (1 − dn )P − d(1 − dn−1 )I2
1−d
un vn
u v
4. Définition : Soit (Qn ) une suite de matrice, où pour tout n ∈ N, Qn =
et soit L =
.
wn x n
w x
On dit que la suite de matrices (Qn ) converge vers la matrice L si et seulement si les quatre suites (un ),
(vn ), (wn ) et (xn ) convergent et ont pour limites respectives u, v, w, x lorsque n tend vers l’infini.
Montrer que la suite (P n ) converge vers une matrice L que l’on explicitera. L appartient-elle à S ?
5. Donner une condition nécessaire et suffisante pour qu’une matrice P de S ne soit pas inversible.
Montrer qu’elle vérifie alors : ∀n > 1, P n = P
Partie II :
Un point mobile M se déplace dans le plan sur deux points A(1, 0) et B(−1, 0).
A l’instant 0, il est en A ou en B, avec équiprobabilité. Puis si à l’instant n il est en A, alors à l’instant n + 1,
il y reste avec probabilité p ∈]0, 1[, et si à l’instant n il est en B, il y reste à l’instant n + 1 avec probabilité
q ∈]0, 1[. On note an (resp. bn ) la probabilité que le mobile soit en A (resp. en B) à l’instant n.
an+1
an
1. Montrer qu’il existe une matrice P ∈ S telle que : ∀n > 1,
=P
bn+1
bn
an
n
2. En déduire alors une expression de
en fonction de P .
bn
3. A l’aide de la partie I, expliciter an et bn en fonction de n. Calculer lim an .
n→+∞
Exercice 4: tout début Essec E 2002
Partie I Résolution de l’équation x2 + x − 1 = 0 (0 < x < 1)
On considère dans cette question la fonction f définie pour x ≥ 0 par : f (x) =
1
x+1
1. Montrer que l’équation x2 + x − 1 = 0 a une seule racine réelle appartenant à [1/2, 1] et préciser la valeur
de r2 . En déduire que r2 est l’unique solution de l’équation f (x) = x sur [1/2, 1]
2. Montrer, si x désigne un nombre réel appartenant à [1/2, 1] , que f (x) appartient à [1/2, 1]
3. Prouver l’inégalité suivante pour 1/2 ≤ x ≤ 1 :|f 0 (x)| ≤
4
9
4. On considère la suite définie par u0 = 1 et un+1 = f (un )
a) Montrer que pour tout entier n, un ∈ [1/2, 1]
b) Prouver alors :∀n ∈ N, |un+1 − r2 | ≤ 94 |un − r2 | puis ∀n ∈ N, |un − r2 | ≤
c) en déduire la convergence de la suite u vers r2 .
4 n
9 .
Partie II Résolution numérique de l’équation x3 + x2 + x − 1 = 0 (0 < x < 1)
1. Montrer que l’équation x3 + x2 + x − 1 = 0 possède une unique solution sur ]0, 1[ que l’on notera r3 .
1
2. On introduit alors la fonction f (x) = x2 +x+1
ainsi que la suite (un ) définie par u0 = 1 et pour tout n ∈ N,
un+1 = f (un ). On admet que par un procédé analogue à la partie I, on a le résultat suivant :
135
∀n ∈ N, |un − r3 | ≤ k n où k = 169
.
Ecrire un programme en scilab qui fournit une valeur approchée à 10−3 près de r3 .
Partie III
On désigne par N un nombre entier supérieur à 1 et par a un nombre réel strictement positif. On note fN la
fonction polynôme définie par fN (x) = xN + xN −1 + · · · + x2 + x − a.
1. Montrer que l’équation fN (x) = 0 possède une racine strictement positive xN et une seule, puis montrer
que celle-ci appartient à ]0, 1[ lorsque N > a
2. Montrer la relation (∗) : (x − 1) fN (x) = xN +1 − (a + 1) x + a
3. Déterminer le signe de fN +1 (x) − fN (x) pour x ∈]0, 1[. En déduire la monotonie de la suite (xN ).
4. Montrer que la suite (xN ) converge vers un nombre x∗ appartenant à [0, 1[
5. Montrer que 0 < xN ≤ xA , puis que 0 < (xN )N ≤ (xA )N lorsque N ≥ A où A est un entier non nul.
En choisissant A ≥ a, en déduire la limite de la suite xN N lorsque N tend vers +∞, puis, à l’aide de la
relation (∗) , exprimer la limite x∗ en fonction de a.