Feuille d`exercices : Ondes sonores

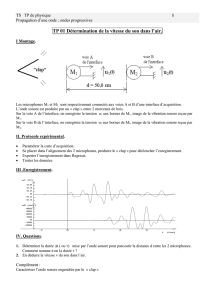
x S
M
◦ρ0
L= 1,45 x=L
ξ(t) = ξ0cos ωt x = 0

x t
V=αp< p2
a>
p(x, t)
f x1xii
x= 0 i
λ
c γ =cp
cv
x= 0
p1(M, t)µ1(M, t)v(M, t)r
t f(r, t) ∆f=1
r2
∂
∂r r2∂f ∂r 
p1(r, t)
p1=p0
rexp i(ωt −kr)
I
Z=p1
vµ0c kr
r0
r(t) = r0+acos(ωt)ar0

p0a r0P
a r0
a
r0= 5
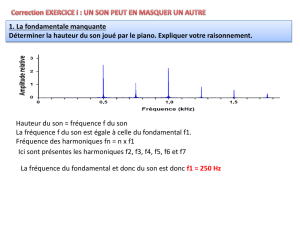
f= 50 I= 90
r= 1
ρ e
x= 0 S
◦ρ0= 1,2−3
x < 0
vi=v0exp j(ωt−kx)
x= 0
x= 0
x < 0
x > 0
τ(jω)
T(ω)
τ(jω)
ρ= 1 800 −3
S x
x= 0 µ0
c m
t= 0 x= 0 x u0

u(t)
p1(x, t)
v1(x, t)
p0
u(t)
τ m S
v1(x, t)t > 0
Lcτ
v1(x, t)t L/c
x S(x)
p0
µ0p(x, t) = p0+pa(x, t)
µ(x, t) = µ0+µa(x, t)~va(x, t)
χS
~va=v0exp i(kx −ωt)~ex
S(x) = S0exp x
aa
λ
[x, x + dx]
k2
i
k
a=ω2 c2
c

fc
a c
S(x)