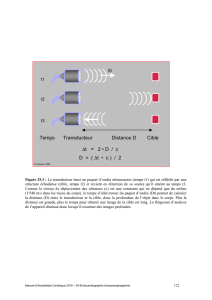
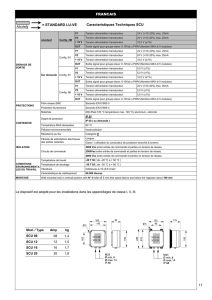
transducteurs et additionneurs

A
L(A)
π n
π n ∈
AnApΣ = {0,1}L(An)
L(Ap)An
L(An) = {n1, n2, . . .}
L(Ap) = {p1, p2, . . .}
An⊕Ap
n∈L(An)p∈L(Ap)L(An⊕Ap) =
{n+p|n∈L(An), p ∈L(Ap)}
An⊕ApO((N×P)2)N
AnP Ap
T
qi/o −−→ q0i
o i
o o i
T ω
T
T
qi −→ q0qi/o −−→ q0
Li(T) = L(Input(T)) Input(qi/o −−→ q0) = qi −→ q0
T
qo −→ q0qi/o −−→ q0

Lo(T) = L(Output(T)) Output(qi/o −−→ q0) = qo −→ q0
TΣ = {0,1}
TΣ = {0,1}
TΣ = {0,1}
A T
A T
A T T
(qa, qt)i/o −−→(q0
a, q0 t)∈A×T qai
−→ q0
a∈A qt
i/o
−−→ q0
t∈T
A T A
A×T
=Output(A×T)
A
(1) ≡(1)2≡(1.0.0.0.0)2≡(1.0∗)2/∈L(A)
(2) ≡(0.1)2≡(0.1.0∗)2∈L(A)
(3) ≡(1.1)2≡(1.1.0∗)2/∈L(A)
A=//?>=<89:;
a0
0//GFED@ABC?>=<89:;
a0
1
0
LL
1
A T
A×T=//?>=<89:;
a0//?>=<89:;76540123
a0
0
JJ
1
×//?>=<89:;/.-,()*+
q
0/1
II
1/0
≡//ONMLHIJK
(a,q)
0/1//ONMLHIJKGFED@ABC
(a0,q)
0/1
II
1/0

A T
Output(A×T) = //ONMLHIJK
(a,q)1//ONMLHIJKGFED@ABC
(a0,q)
1
II
0
≡
An⊕Ap
ApTp
AnTp
An⊕Ap=Output(An×Tp)
n p
111111 = n
+ 11 = p
0100001
−−−−−−−−→
111111 retenue
1111110 = n
+ 1100000 = p
0100001
p p.0∗p0
Ap
ApΣ = {0,1}
pL(Ap)
A=//?>=<89:;
a0
1//?>=<89:;76540123
a1
ApAp
/.-,()*+ ///.-,()*+
0
EE
1
−→ 0 −→ Ap
+1
−−→ +0 −−→
Ap//?>=<89:;
a0
1//?>=<89:;76540123
a1//?>=<89:;76540123 a2
0
HH//?>=<89:;
a0
1//?>=<89:;76540123
a2
0
HH
A⊕
p=//?>=<89:;
a0
+1 //?>=<89:;76540123
a2
+0
HH

+?
−−→
q+1 −−→ q00/.. −−→
1/..
−−→
(q, r = 0)
(q, r = 1)
q+1 −−→ q0
(q, r = 0) 0/1 −−→
+1(q0, r = 0) r= 0 + 1 r= 0
(q, r = 0) 1/0 −−→
+1(q0, r = 1) r= 0 + 0 r= 1
(q, r = 1) 0/0 −−→
+1(q0, r = 1) r= 1 + 0 r= 1
(q, r = 1) 1/0 −−→
+1(q0, r = 1) r= 1 + 1 r= 1
q+0 −−→ q0
(q, r = 0) 0/0 −−→
+0(q0, r = 0) r= 0 + 0 r= 0
(q, r = 0) 1/1 −−→
+0(q0, r = 0) r= 0 + 1 r= 0
(q, r = 1) 0/1 −−→
+0(q0, r = 0) r= 1 + 1 r= 0
(q, r = 1) 1/0 −−→
+0(q0, r = 1) r= 1 + 0 r= 1
T A
(q, r = 0) q
A⊕
p=//?>=<89:;
a0
+1 //?>=<89:;76540123
a2
+0
HH
Tp=//WVUTPQRS
(a0,r=0)
0/1
+1 //
1/0+1
WVUTPQRSONMLHIJK
a2,r=0
+0: 0/0,1/1
WVUTPQRS
(a2,r=1)
+0
0/1
99
s
s
s
s
s
s
s
s
s
s
s
+0: 1/0
VV
Tp=///.-,()*+ 0/1//
1/0
/.-,()*+
0/0,1/1
/.-,()*+ 0/1
??
1/0
YY
T A Σ = {0,1}

q+0 −−→ q0∈Ap=⇒
(q, r = 0) 0/0,1/1 −−−−−→(q0, r = 0)
(q, r = 1) 0/1 −−→(q0, r = 0)
(q, r = 1) 1/0 −−→(q0, r = 1)
∈Tp
q+1 −−→ q0∈Ap=⇒
(q, r = 0) 0/1 −−→(q0, r = 0)
(q, r = 0) 1/0 −−→(q0, r = 1)
(q, r = 1) 0/0 −−→(q0, r = 1)
(q, r = 1) 1/1 −−→(q0, r = 1)
∈Tp
q∈Init(Ap) =⇒(q, r = 0) ∈Init(Tp)
q∈Acc(Ap) =⇒(q, r = 0) ∈Acc(Tp)
(. . . , r = 1)
An
An=//?>=<89:;
a0
0//GFED@ABC?>=<89:;
a0
1
0
LL
1
≡0.(1|0)∗
TpAp=//GFED@ABC
a01//GFED@ABC a11//GFED@ABC?>=<89:; a2
0
AnTp
{n+p|n∈L(An), p ∈L(Ap)}