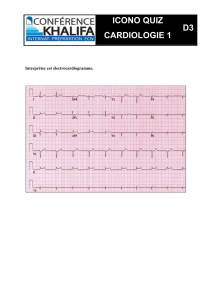
E inf

L’essentiel sur les ondes
1. Les ondes électromagnétiques (Rappel)
1.1. Définitions
Définition :
Une onde électromagnétique est la propagation d’une perturbation électromagnétique (combinaison d’un champ
magnétique et d’un champ électrique) dans un milieu (modification de l’état des électrons dans les atomes).
Une onde électromagnétique se caractérise par :
- Sa vitesse de propagation dans le milieu (en m.s1) aussi appelée célérité ;
- Sa période T (en s) et sa fréquence (
1
) ( =
1
T
, en Hz), si elle est périodique ;
- Sa longueur d'onde λ (en m) qui correspond à la distance parcourue par l’onde pendant la durée T :
-1
v vitesse de propagation de l'onde (en m.s )
T période de l'onde (en s)
ν fréquence de l'onde (en Hz)
v
vT ν ==
Remarque : dans le vide, la vitesse de propagation d’une onde électromagnétique est égale à la célérité de la lumière
dans le vide : c = 299 792 458 m.s–1.
On a alors :
-1
célérité de la lumière dans le vide (en m.s )
T période de l'onde (en s)
ν fréquence de l'onde (en Hz)
Tν
c
c
c ==
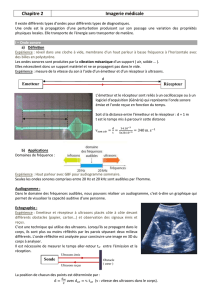
1.2. Spectre des ondes électromagnétiques
Les ondes électromagnétiques sont classées en plusieurs domaines qui sont fonction de leur fréquence ou de leur
longueur d'onde dans le vide :
1
Lettre grecque « nu »

2. Les ondes mécaniques
2.1. Les ondes mécaniques progressives
Définition :
On appelle « onde mécanique progressive », le phénomène de propagation de proche en proche d’une perturbation
(modification locale et temporaire du milieu) dans un milieu matériel sans transport de matière.
Remarques :
 Une onde mécanique transporte de l’énergie mais pas de matière ;
 Une onde se « propage », à partir de la source, dans toutes les directions qui lui sont offertes. On
distinguera ainsi les ondes à une, deux ou trois dimensions : une onde progressive se propageant dans une
seule direction sera appelée « onde progressive à une dimension », une onde se propageant dans un plan
sera appelée « onde progressive à deux dimensions », etc.
 Dans le cas des ondes mécaniques, un point est repéré par son élongation, c'est-à-dire sa position par
rapport à sa position de repos.
2.1.1. Les ondes mécaniques transversales
Définition :
On appelle « onde mécanique transversale », une onde mécanique dont la direction de propagation est
perpendiculaire à la direction de la perturbation qui l’a fait naitre.
Exemples : onde à la surface de l’eau (), ondes S d’un séisme (), …
2.1.2. Les ondes mécaniques longitudinales
Définition :
On appelle « onde mécanique longitudinale », une onde mécanique dont la direction de propagation est parallèle à
la direction de la perturbation.
Exemples : ondes sonores (), ondes P d’un séisme ()
2.2. Célérité d’une onde
Définition :
On appelle célérité v d’une onde sa vitesse de propagation. C'est le rapport entre la distance d parcourue par l'onde et
la durée t du parcours :
distance parcourue (en m)
durée du parcours (en s)
célérit é (en m /s)
d
t
d
vtv
Remarque :
Lorsqu’une perturbation se propage entre un point M et un point M’ d’un milieu de propagation, la durée  que met
cette perturbation pour parcourir la distance MM’ est appelée retard :

1
MM' distance (en m)
retard (en s)
v vitesse (en m.s )
MM'
v= τ
Remarques :
 Une onde mécanique nécessite un support matériel (milieu matériel) pour se propager contrairement aux
ondes électromagnétiques qui peuvent se propager dans le vide ;
 Un milieu peut absorber une partie de l’énergie transportée par la perturbation qui s’y déplace : on dit qu’il y
a amortissement, les caractéristiques de l’onde sont alors modifiées.
2.3. Les ondes mécaniques (progressives) périodiques
Définitions :
 La période d'un phénomène périodique est la durée au bout de laquelle le phénomène se répète identiquement à
lui-même. On la note T et elle s'exprime en secondes (symbole : s) ;
 La fréquence d'un phénomène périodique représente le nombre de répétitions du phénomène par seconde. On la
note généralement f et elle s’exprime en hertz (symbole : Hz) ;
La fréquence et la période sont reliées par la relation :
1
T
f
 Une onde mécanique est dite périodique lorsque la perturbation se reproduit identiquement à elle-même à
intervalles de temps égaux, appelés période temporelle T.
Remarques :
 La période temporelle d’une onde est la durée qui sépare deux perturbations consécutives, c’est sa période ;
 La longueur d’onde = distance parcourue par l’onde pendant une durée égale à sa période T.
= période spatiale de l'onde progressive périodique.
 Relation entre élongations :
 Les points M, M' et M'' conservent la même élongation quelque soit l'instant t. On dit que les points M, M' et M''
vibrent en phases.
 Relation entre période et longueur d'onde :
La longueur d'onde λ correspond à la plus petite distance séparant deux positions de l’onde pour lesquelles les
élongations sont en phase. C'est aussi la distance parcourue par l'onde pendant une durée égale à sa période
temporelle T :
On sait que :
d
vtT
 = v  T =
v
f
Une onde présente donc une double périodicité :
- une périodicité temporelle de période T (exprimée en secondes).
- une périodicité spatiale de période  (exprimée en mètres).
Front de l’onde

2.4. Les ondes mécaniques progressives sinusoïdales
Dans le cas d'une onde mécanique sinusoïdale l'évolution de l'élongation d’un point, du milieu où se propage l’onde,
au cours du temps x(t) est une fonction sinusoïdale. Elle peut, par exemple, être modélisée par une fonction
mathématique de la forme :
max
max
X amplitude (en m)
2π
( ) X cos T période (en s)
Tphase à l'origine (en rad)
x t t
Si pour t = 0, l’élongation x(t = 0) = Xmax alors  = 0.
Remarque : un milieu matériel dans lequel la célérité des ondes sinusoïdales dépend de leur fréquence est appelé
milieu dispersif :
2.5. Les ondes sonores
Définition :
Une onde sonore est la propagation d’un phénomène périodique constitué d’une suite de compressions et de
dilatation du milieu de propagation. Il s’agit d’une onde mécanique progressive qui se propage dans un milieu
matériel mais pas dans le vide.
Domaines de fréquences des ondes sonores :
2.5.1. Acoustique musicale
Définition :
- Si l’enregistrement d’une onde sonore donne un signal sinusoïdal alors le son est qualifié de son pur ;
- Si l’enregistrement d’une onde sonore donne un signal périodique (non sinusoïdal) alors le son est qualifié de
son complexe.
" "

Exemples :
Un son pur est un son obtenu à partir d’une seule fréquence
Un son complexe est la superposition de plusieurs sons purs
2.5.1.1. Caractéristiques d’un son
En acoustique, on distingue pour les sons musicaux, trois qualités physiologiques : la hauteur, le timbre et l’intensité.
La hauteur d'un son correspond entre autres à sa fréquence de vibration. Plus la vibration est rapide, plus le son est
dit aigu ; au contraire, plus la vibration est lente, plus le son est dit grave. Le seuil de reconnaissance de la hauteur
est défini à 1/100e de seconde en moyenne (pour des fréquences de l'ordre de 440 Hz) pour l'homme. Plus bref, le
son perçu n’a pas de hauteur définie et est qualifié par les acousticiens de « claquement ».
Le timbre est en quelque sorte la « couleur » propre d’un son, il permet de différencier deux notes de même hauteur
jouées par des instruments différents. Il dépend de :
On définit l’intensité acoustique (ou sonore), notée I, par la puissance acoustique (ou puissance sonore) reçue par
unité de surface du récepteur ; elle s'exprime en watt par mètre carré (symbole : W.m²).
2
I
I
P puissance acoustique de la source (en W)
PS surface du récepteur (en m²)
Sintensité acoustique (en W.m )
 L'intensité acoustique minimale perçue par l'oreille humaine est de l'ordre de 10−12 W.m² : c'est le seuil
d'intensité acoustique.
 L'intensité acoustique maximale perçue par l'oreille humaine est de l'ordre 25 W.m² : c’est le seuil de douleur. Au-
delà, il y a destruction du tympan.
 L’intensité acoustique d’un son est liée à l’amplitude de l’onde sonore.
Remarque : L’enveloppe d’un son traduit l’évolution de l’amplitude du signal sonore. Elle contribue également au
timbre de l’instrument.
On distingue plusieurs phases dans l’enveloppe d’un son :
- L’attaque, pendant laquelle l’amplitude du son augmente ;
- Le corps, pendant laquelle l’amplitude reste à peu près constante ;
- L’extinction, pendant laquelle l’amplitude diminue jusqu’à s’annuler.
INTENSITE ACOUSTIQUE
TIMBRE
HAUTEUR