devoir n°3 - ambition

!
Page%1!
!
!
!
1"
LFA%/%DS%mathématiques%TSA%-%TSB%2014%-%2015%
Exercice 1 : commun à tous les candidats
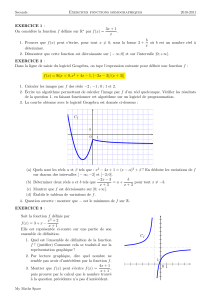
Sur$le$graphique$ci-dessous,$on$a$tracé,$dans$le$plan$muni$d’un$repère$orthonormé$
O;
i; j
( )
,$la$courbe$représentative$
Cf
$
d’une$fonction$
f
$définie$et$dérivable$sur$l’intervalle$
0 ; +∞
⎤
⎦⎡ ⎣
.$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
On$dispose$des$informations$suivantes$:$
• les$points$
A;B;C
$ont$pour$coordonnées$respectives$
1; 0
( )
$;$
1; 2
( )
$;$
0 ; 2
( )
$;$
• la$courbe$
Cf
$passe$par$le$point$
B
$et$la$droite$
BC
( )
$est$tangente$à$
Cf
$en$
B
$;$
• il$existe$deux$réels$positifs$
a
$et$
b
$tels$que$pour$tout$réel$strictement$positif$
x
,$$
f x
( )
=a+bln x
x
.$
1) a$/$En$utilisant$le$graphique,$donner$les$valeurs$de$
f1
( )
$et$
′
f1
( )
.$
b$/$Vérifier$que$pour$tout$réel$strictement$positif$
x
,$
′
f x
( )
=b−a
( )
−bln x
( )
x2
.$
c$/$En$déduire$les$réels$
a
$et$
b
.$
2) a$/$Justifier$que$pour$tout$réel$
x
$appartenant$à$l’intervalle$
0 ; +∞
⎤
⎦⎡ ⎣
,$
′
f x
( )
$a$le$même$signe$que$
−ln x
( )
.$
b$/$Déterminer$les$limites$de$
f
$en$
0
$et$en$
+∞
.$On$pourra$remarquer$que$pour$tout$réel$
x
$strictement$positif,$$
$$$$$$$
f x
( )
=2
x+2ln x x
.$
c$/$En$déduire$le$tableau$de$variations$de$la$fonction$
f
.$
3) a/Démontrer$que$l’équation$
f x
( )
=1
$admet$une$unique$solution$
α
$sur$l’intervalle$
0 ;1
⎤
⎦⎡ ⎣
.$
b$/$Par$un$raisonnement$analogue,$on$démontre$qu’il$existe$un$unique$
β
$de$l’intervalle$
1; +∞
⎤
⎦⎡ ⎣
$tel$que$$
$$$$$$
f
β
( )
=1
$
$$$$$$$Déterminer$l’entier$
n
$tel$que$
n<
β <n+1
.$
4) On$donne$l’algorithme$ci-dessous$:$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$

!
Page%2!
!
!
!
2"
LFA%/%DS%mathématiques%TSA%-%TSB%2014%-%2015%
$
$a$/$Faire$tourner$cet$algorithme$en$complétant$le$tableau$ci-dessous$que$l’on$recopiera$sur$la$copie$
$
$
$
$
$
$
$
$
$
$b$/$Que$représentent$les$valeurs$affichées$par$cet$algorithme$?$
$c$/$Modifier$l’algorithme$ci-dessus$pour$qu’il$affiche$les$deux$bornes$d’un$encadrement$de$
β
$d’amplitude$
10−1
.$
$
$
Exercice 2 : commun à tous les candidats
Cet$exercice$est$un$questionnaire$à$choix$multiples.$Pour$chacune$des$questions,$une$seule$réponse$est$exacte.$$
Le$candidat$indiquera$sur$la$copie$la$réponse$choisie.$Chaque"réponse"devra"être"rigoureusement"justifiée.$
L’absence$de$justification$ne$sera$pas$prise$en$compte$
1) Soit$
z1=6e
i
π
4
$et$
z2=2e
−i
π
3
.$La$forme$exponentielle$de$
i
z1
z2
$est$:$
a.$$
3e
i19
π
12
$b.$$
12e
−i
π
12
$c.$$
3e
i7
π
12
$d.$$
3e
i13
π
12
$
2) L’équation$
−z=z
,$d’inconnue$
z
,$admet$:$
a."$une$solution$
b.$$deux$solutions$
c.$$une$infinité$de$solutions$dont$les$points$images$dans$le$plan$complexe$sont$situés$sur$une$droite.$
d.$$une$infinité$de$solutions$dont$les$points$images$dans$le$plan$complexe$sont$situés$sur$un$cercle.$
3) Dans$un$repère$de$l’espace,$on$considère$les$trois$points$
A1; 2 ; 3
( )
,$
B−1; 5 ; 4
( )
$et$
C−1; 0 ; 4
( )
.$
La$droite$parallèle$à$la$droite$
AB
( )
$passant$par$le$point$
C
$a$pour$équation$paramétrique$:$
$
$
$
$
$
$
$
$
4) Le$plan$est$rapporté$au$repère$orthonormal$direct$
O;
u; v
( )
.$On$considère$les$points$
A;B;C
$d’affixes$
respectives$:$$$$
a=2+2i
$;$$
b=−3+i
$;$$
c=1+i3
.$
a."$les$droites$
AB
( )
$et$
AC
( )
$sont$perpendiculaires.$
b.$$le$triangle$
ABC
$est$équilatéral$
c.$$les$points$
A;B;C
$sont$alignés$
d.$$le$triangle$
ABC
$est$isocèle$en$
A
$
$
$
$
$

!
Page%3!
!
!
!
3"
LFA%/%DS%mathématiques%TSA%-%TSB%2014%-%2015%
$
Exercice 3 : commun à tous les candidats
$
On$note$
un
( )
$et$
vn
( )
$les$suites$réelles$définies,$pour$tout$entier$naturel,$par$:$
$ $ $
u0=1
$;$$
v0=0
$$et$$
un+1=3un−vn
vn+1=un+3vn
⎧
⎨
⎪
⎩
⎪
$
$
1) Calculer$les$valeurs$de$
u1,v1,u2,v2
.$
2) On$souhaite$construire$un$algorithme$qui$affiche$les$valeurs$de$
uNet vN
$pour$un$entier$naturel$
N
$donné.$
a$/$On$donne$l’algorithme$suivant$:$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$$$$$$$$$Faire$fonctionner$cet$algorithme$pour$
N=2
.$Pour$cela,$on$recopiera$et$complétera$le$tableau$de$variables$
$$$$$$$$$ci-dessous$:$
$
$
$
$
$
$
$
$b$/$L’algorithme$précédent$affiche-t-il$les$valeurs$de$
uNet vN
$pour$un$entier$
N
$donné$?$
$$$$$$$$Dans$le$cas$contraire,$écrire$sur$la$copie$une$version$corrigée$de$l’algorithme$proposé$qui$affiche$bien$les$$$$$$$
$$$$$$$$$$$$$$$$$$$$$$$valeurs$de$
uNet vN
$pour$un$entier$naturel$
N
.$
3) On$pose,$pour$tout$entier$naturel$
n
,$
zn=un+ivn
.$
On$note$
a=3+i
.$
a$/$Démontrer$que,$pour$tout$entier$naturel$
n
$:$
$$$$$$
zn+1=azn
$
b$/$Écrire$
a
$sus$la$forme$exponentielle.$
c$/$En$déduire$que,$pour$tout$entier$naturel$
n
$:$$
$$$$$
un=2ncos n
π
6
⎛
⎝
⎜⎞
⎠
⎟
vn=2nsin n
π
6
⎛
⎝
⎜⎞
⎠
⎟
⎧
⎨
⎪
⎪
⎩
⎪
⎪
$
$

!
Page%4!
!
!
!
4"
LFA%/%DS%mathématiques%TSA%-%TSB%2014%-%2015%
$
$
$
Exercice 4 : candidats n'ayant pas suivi l'enseignement de spécialité)
$
Le$plan$est$rapporté$à$un$repère$
O;
i; j
( )
$
Soit$a$un$nombre$réel$strictement$positif$
On$note$∆a$la$droite$d’équation$y$=$ax$et$Γ$la$courbe$représentative$de$la$fonction$exponentielle$dans$le$repère$orthonormal$
repère$
O;
i; j
( )
$
Le$but$de$cet$exercice$est$de$déterminer$le$nombre$de$points$d’intersection$de$Γ$et$de$∆a$suivant$les$valeurs$de$a.$
Pour$cela,$on$considère$la$fonction$fa$définie$pour$tout$nombre$réel$x%par$:$ $
$$$$$$$$fa(x)$=$ex$–$ax.$
On$admet$pour$tout$réel$a$que$la$fonction$fa$est$dérivable$sur$l’ensemble$des$nombres$réels.$
$
1) Etude"du"cas"particulier$a$=$2$
$$$$$La$fonction$f2$est$donc$définie$pour$tout$réel$x$réel$par$f2(x)$=$ex$–$2x.$
a) Etudier$les$variations$de$la$fonction$f2$sur$l’ensemble$des$réels$et$dresser$son$tableau$de$variation$sur$
l’ensemble$des$réels.$(on$ne$demande$pas$de$déterminer$les$limites$aux$bornes$de$l’ensemble$de$définition).$
b) En$déduire$que$Γ$et$de$∆2$n’ont$pas$de$point$d’intersection.$
$
2) Etude"du"cas"général"où"a"est"un"réel"strictement"positif."
a) Déterminer$les$limites$de$la$fonction$
fa
$en$+$∞$et$en$–$∞.$
b) Etudier$les$variations$de$la$fonction$fa$sur$l’ensemble$des$réels.$$
Montrer$alors$que$le$minimum$sur$l’ensemble$des$réels$de$la$fonction$fa%$est$$a$–$$a%ln$a.$
c) Etudier$le$signe$de$a$–$$a%ln$a%suivant$les$valeurs$du$réel%a.$
d) Déterminer$selon$les$valeurs$du$réel$
a
$le$nombre$de$points$communs$à$Γ$et$de$∆a.$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
$
!
$
$
$