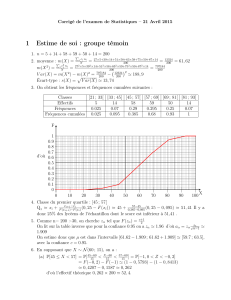
Distribution des fréquences

La statistique descriptive

Plan
Distribution de fréquences
Distribution de fréquences cumulatives
Mesures de la tendance centrale
Mesures de variabilité

Distribution des fréquences
Définition: C’est une liste de valeurs dans un
échantillon.
Exemple:
x= {60, 38, 41, 45, 40, 75, 31, 35, 45, 46, 55, 61, 40, 15, 58, 71, 46, 53, 65, 54, 41,
56, 45, 65, 69, 50, 54, 41, 57, 44, 75, 30, 44, 30, 63, 44, 58, 34, 33, 66, 49, 42, 58,
70, 28, 49, 47, 47, 58, 38}
Habituellement, pour des fins de visualisation, la liste est
regroupée en classe.

Distribution des fréquences
Largeur des classes = 1

Distribution des fréquences
Largeur des classes = 5