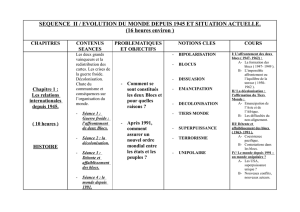
1. Creuser une rivière artificielle à moindre coût 3 pts 2. Utilisation

π(x)s x
π(x) = min
y∈N−(x)(π(y) + c(yx)).
π(s)=0 π(a)=3sπ(b)=8aπ(c)=9sπ(d) = 21bπ(f) = 20bπ(k) = 24fπ(g) = 26d
π(e) = 32dπ(i) = 44eπ(h) = 29gπ(l) = 37hπ(m) = 51lπ(n) = 54hπ(o) = 59nπ(q) = 38kπ(j) = 42e
π(r) = 55qπ(p) = 58jπ(t) = 64p
s−a−b−d−e−j−p−t
τi
tji tj+1 i0τi> τi0
f(tj+τi) + f(tj+1 +τi0)
f(tj+1 +τi0)−f(tj+τi0)≤f(tj+1 +τi)−f(tj+τi),
f(tj+τi) + f(tj+1 +τi0)≤f(tj+1 +τi) + f(tj+τi0).
i i0
Pn−1
i=1 ρui+Po∈O Pn−qo i=1 γovi,o
kPn
i=1 xi,k =nki∈ {1, . . . , n}Pk∈K xi,k = 1
yi,c =Pk∈K k,cxi,k i∈ {1, . . . , n}c∈ C
zi,o =Pk∈K δk,oxi,k i∈ {1, . . . , n}o∈ O
Pi+r−1
j=iuj≥1i∈ {1, . . . , n −r+ 1}
Pi+r
j=iyj,c ≤r i ∈ {1, . . . , n −r}
c∈ C
i c ui≥yi,c −yi+1,c ui≥yi+1,c −yi,c i
o vi,o ≥Pi+qo−1
j=izj,o −po

min Pn−1
i=1 ρui+Po∈O Pn−qo i=1 γovi,o
Pn
i=1 xi,k =nkk∈ K
Pk∈K xi,k = 1 i∈ {1, . . . , n}
yi,c =Pk∈K k,cxi,k i∈ {1, . . . , n}, c ∈ C
zi,o =Pk∈K δk,oxi,k i∈ {1, . . . , n}, k ∈ K
Pi+r−1
j=iuj≥1i∈ {1, . . . , n −r+ 1}
ui≥yi,c −yi+1,c i∈ {1, . . . , n −1}, c ∈ C
ui≥yi+1,c −yi,c i∈ {1, . . . , n −1}, c ∈ C
vi,o ≥Pi+qo−1
j=izj,o −poo∈ O, i ∈ {1, . . . , n −qo+ 1}
ui, yi,c, zi,o, xi,k ∈ {0,1}
vi,o ∈Z+.
xi,k =nk/n i k
bn/rcρ
min Pn−1
i=1 ρui
Pi+r−1
j=iuj≥1i∈ {1, . . . , n −r+ 1}
ui∈ {0,1}.
bn/rcρ
r= +∞qo= 2 o∈ O
ij
ij
qo= 2
cij =ρ×1i j +X
o∈O
γo×1i j o po= 1
1 3
2 5×1+2 = 7
1,4,6,2,7,5,3 7
O=∅
∗mc∗
c∗
c6=c∗
mc∗−1≤X
c∈C\{c∗}
Nc.
c
mcc mc
≤r

mc∗−1≤Pc∈C\{c∗}mcc6=c∗
c∗
mcc c ∈ C
Pc∈C mc−1
mc∗−1>Pc∈C\{c∗}mcmc< mc∗c
c6=c∗=mc∗−1
2mc∗−2
Pc∈C mc
Pc∈C mc−1
c∗2 2mc∗−2
c t(c)= 2
K(c)−k(c)
1g(`)
z=z0h0> h z h
h0
z6=z0c j z =z(c)
jh=h(c) jz0=z(c) j+1 h0=h(c) j+1
c z h z0h0
z=z0Qa= +∞Qa=K(c)−k(c)
jc j
max X
`∈L
g(`)y(`)
X
`∈L
κ(`)x(`)
a≤Qaa∈A
X
a∈δ+(v)
x(`)
a=X
a∈δ−(v)
x(`)
a`∈L, v ∈V\ {v(`)
o, v(`)
d}
X
a∈δ+(v(`)
o)
x(`)
a=y(`)`∈L
x(`)
a, y(`)∈ {0,1}.
x(`)
a, y(`)∈ {0,1}x(`) a, y(`)∈[0,1]
−P`∈Lg(`)y(`)

G(λ) = min −X
`∈L
g(`)y(`)+X
`∈L
X
a∈A
λa(κ(`)x(`)
a−Qa)
X
a∈δ+(v)
x(`)
a=X
a∈δ−(v)
x(`)
a`∈L, v ∈V\ {v(`)
o, v(`)
d}
X
a∈δ+(v(`)
o)
x(`)
a=y(`)`∈L
x(`)
a, y(`)∈ {0,1}.
` `
G(λ)g κ λaQa
a∈A vo, vdG
min −gy +X
a∈A
λaκxa
X
a∈δ+(v)
xa=X
a∈δ−(v)
xav∈V\ {vo, vd}
X
a∈δ+(vo)
xa=y
xa, y ∈ {0,1}.
G
a λaκ < g
xay= 1 y=xa= 0 a∈A
G(λ)
G(λ)