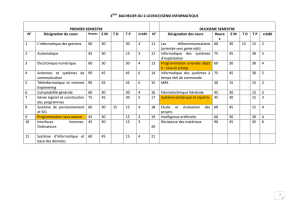
Une hypersurface admettant une normale unitaire lisse est orientée.

V⊂RnN:V→Sn−1
H E
v H O
H(b1, . . . , bn−1)H
(b1, . . . , bn−1, v)E
H v E
x V N(x)
Rn
OxTxV
(Ox)x∈V
V y Oy
Rn−1
x V φ :U→Rn−1
V x DxφOx
φ L ◦φ L
Rn−1
φ Dxφ Dyφ
y x
B
B B
B
B B
(b1(x), . . . , bn−1(x)) TxV
(Dxφ(b1(x)), . . . , Dxφ(bn−1(x))) Rn−1
y x bi(y) := Dyφ−1Dxφ(bi(x))
16i6n−1 (b1(y), . . . , bn−1(y)) TyV
O(x) (b1(x), . . . , bn−1(x))
(b1(x), . . . , bn−1(x), N(x)) Rny x
(b1(y), . . . , bn−1(y), N(y)) (b1(x), . . . , bn−1(x), N(x))
Rn(b1(y), . . . , bn−1(y))
Oy
y x Dyφ
(b1(y), . . . , bn−1(y)) (Dxφ(b1(x)), . . . , Dxφ(bn−1(x)))
Rn−1y x Dyφ
OyRn−1