TD - Lamsade

MI2E - 1EANNÉE
ALGORITHMIQUE GÉNÉRALE
C. Murat, V. Mousseau
T.D. LES ARBRES
Exercice 1 :
Considérons l’arbre suivant. A
B C
D E F G H
I J K L
M N
a) Quels sont les fils du noeud C?
b) Quel est le père du noeud C?
c) Quel noeud est la racine du graphe ?
d) Quels noeuds sont des feuilles ?
e) Quels noeuds sont les ascendants du noeud C?
f) Quels noeuds sont les descendants du noeud C?
g) Quels sont les frères du noeud C .
h) Quels sont les noeuds à gauche de C? à sa droite?
i) Quelle est la profondeur du noeud C
j) Quelle est la hauteur du noeud C
Exercice 2 : Lister les noeuds de l’arbre de l’exercice 1 suivant un parcours a) préfixé, b) postfixé, c)
infixé.
Exercice 3 : Supposons que les tableaux PREFIXE[n],INFIXE[n]et POSTFIXE[n]donnent la
position de chaque noeud d’un même arbre dans les parcours préfixé, infixé et postfixé, respectivement.
Décrire un algorithme permettant de déterminer si le noeud iest un ascendant du noeud j, quels que
soient les noeuds iet j.
Exercice 4 : Placer une croix à l’intersection de la ligne iet de la colonne jsi les deux conditions
représentées par cette ligne et cette colonne peuvent être réalisées en même temps. Par exemple, on
mettra une croix à l’intersection de la ligne 3 et de la colonne 2 s’il est vrai que npeut être ascendant

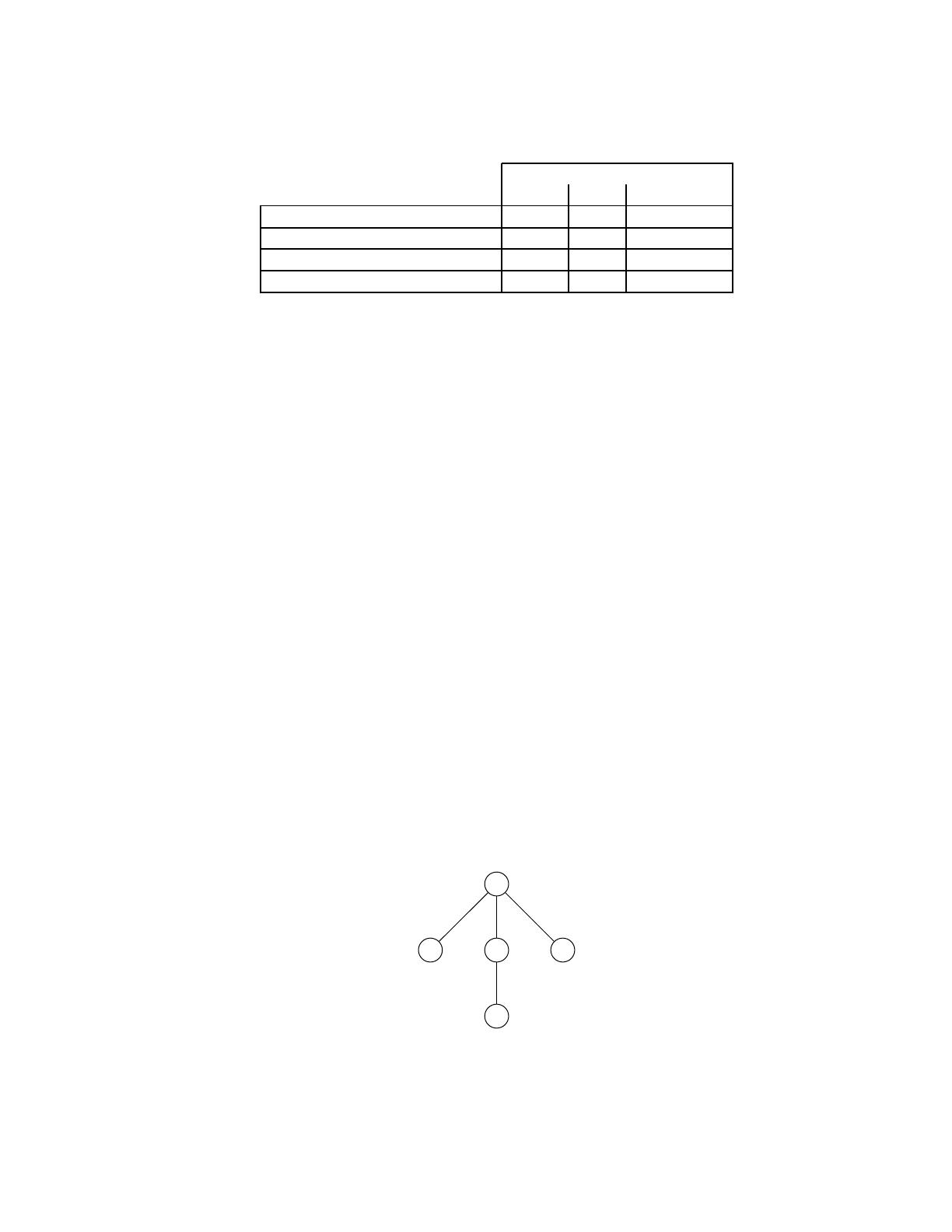
propre de met en même temps que nprécède mdans un parcours infixé.
nest avant mdans un parcours
préfixé infixé postfixé
nest à gauche de m
nest à droite de m
nest un ascendant propre de m
nest un descendant propre de m
Notations et définitions de primitives pour les arbres :
On note nun noeud de l’arbre, eune étiquette d’un noeud et Aun arbre.
–PERE(n,A)retourne le père du noeud ndans l’arbre A. Si nest la racine de A, alors le noeud
vide est retourné.
–PREMIER-FILS(n,A)retourne le fils le plus à gauche du noeud ndans l’arbre A. Si nest
une feuille, alors le noeud vide est retourné.
–FRERE-DROIT(n,A)retourne le frère droit du noeud ndans l’arbre A. Si nest fils unique,
alors le noeud vide est retourné.
–ETIQUETTE(n,A)retourne l’étiquette du noeud ndans l’arbre Aqui est étiqueté.
–CREERi(e, A1, A2, ..., Ai)pour chaque valeur de i=0,1,2, ... , CREERi construit un nouveau
noeud d’étiquette eet lui associe ienfants qui sont les racines des sous-arbres Al,A2,...,Ai
dans cet ordre de gauche à droite. Si i= 0 alors le nouveau noeud est à la fois une feuille et une
racine
–RACINE(A)retourne le noeud qui est racine de l’arbre A, ou le noeud vide si l’arbre Aest
vide
–RAZ(A)transforme l’arbre Aexistant en arbre vide.
Exercice 5 : En prenant la représentation des arbres par tableau des pères, que l’on rappellera, écrire
la primitive FRERE-DROIT(n,A).
Exercice 6 :
Donner la représentation de l’arbre suivant avec la structure “premier-fils, frère-droit” que l’on
précisera.
1
2 3 4
5
Exercice 7 : En prenant la représentation des arbres par liste chaînée des fils, que l’on précisera, écrire
les primitives suivantes :
a) PREMIER-FILS(n,A)
b) PERE(n,A)
c) FRERE-DROIT(n,A)
2

d) RACINE(A)
NB : on pourra, si besoin, utiliser les primitives des listes déjà définies dans les TDs précédents
Exercice 8 : Ecrire la primitive CREER2(e, A1, A2) en prenant la représentation “père, premier-fils,
frère-droit” d’un arbre.
Exercice 9 :
a) Comment définit-on les descendants d’un noeud?
b) Quelles sont les descendants du noeud Bdans l’arbre ci-dessous.
A
C B F
Z I QT D
H EG
J K L M
On souhaite définir une fonction DESCENDANTS(A:arbre, n:noeud) qui prenne en en-
trée un arbre Aet nun noeud de cet arbre, et donne en sortie le nombre de descendants de ce noeud
dans l’arbre.
c) Expliquer la représentation des arbres par tableau des pères et l’illustrer sur l’arbre précédent.
d) En supposant que l’arbre est représenté par tableau des pères, donner la fonction en C de DES-
CENDANTS (arbre A, noeud n)., Quelle est sa complexité? L’appliquer pour le noeud B de
l’arbre donné en b).
e) En supposant que l’arbre est représenté par pointeur du type “père, premier-fils, frère-droit”,
donner la fonction en C de DESCENDANTS (arbre A 1 noeud n). Quelle est sa complexité ?
L’appliquer pour le noeud B de l’arbre donné en b). Vous définirez au préalable correctement
votre structure de données en C et éventuellement les conventions choisies.
Exercice 10 :
a) Donnez la profondeur des noeuds M, H et X dans l’arbre ci-dessous.
b) Soit le type de données suivant pour représenter les arbres :
typedef struct typenoeud
{int étiquette i;
struct typenoeud *pere
struct typenoeud *premier-fils
struct typenoeud *frere-droit
}noeud;
et dans ce cas le type de données “ARBRE” est un pointeur sur la cellule représentant la racine
de l’arbre, c’est-à-dire :
3

X
O C
N D L J H
E G K I
M F Q
B
typedef noeud *arbre i
Donnez la représentation par pointeur et noeud du sous-arbre précédent restreint aux noeuds C,
L, 1, H, G, K, J, Q.
c) En utilisant le type de données défini dans la question b), donnez une fonction qui prend en
entrée le noeud n et l’arbre A et donne en sortie la profondeur de n dans A (vous expliquerez,
de façon" littéraire ", rapidement l’idée de votre fonction).
d) Appliquez votre fonction pour le noeud Q de l’arbre de la question a).
e) Reprendre les questions c) et d) mais en supposant que le pointeur “père” de chaque noeud ne
fasse plus partie de la structure.
Exercice 11 : La longueur du chemin intérieur d’un arbre binaire complet est la somme, restreinte
à tous les noeuds internes de l’arbre, de la profondeur de chaque noeud. De même, la longueur du
chemin extérieur est la somme, restreinte à toutes les feuilles de l’arbre, de la profondeur de chaque
feuille. On considère un arbre binaire complet avec nnoeuds internes, un chemin intérieur de longueur
i, et un chemin extérieur de longueur e. Démontrer que e=i+ 2n(commencer par le vérifier sur 2
ou 3 exemples que vous construirez).
Exercice 12 : On supposera que la mise en oeuvre des arbres binaires est faite par pointeurs “fils-
gauche, fils-droit, père”.
a) Ecrire une fonction récursive qui étant donné un arbre binaire B, imprime l’étiquette de chaque
noeud de l’arbre, selon un parcours préfixé.
b) Ecrire une fonction non récursive qui étant donné un arbre binaire B, imprime l’étiquette de
chaque noeud de l’arbre. Si besoin, vous pouvez utiliser une pile (et les primitives déjà définies
qui lui sont associées) comme structure de données auxiliaire.
c) Appliquez pas à pas vos deux fonctions sur l’arbre suivant
4

1
2
3 4
5
6
7
5