Chapitre 1— Séries numériques 1 Exemples fondamentaux 2

MVA101 Analyse et calcul matriciel
Jacques Vélu (CNAM)
Chapitre 1— Séries numériques
1
Exemples fondamentaux
1+
1. La série harmonique :
S1 S2
1 1 1
1
+ + + ··· + + ···
2 3 4
n
S4
S8
S16
S32
0
S64
S128 S256 S512
S1024
4
1
1
1
1
1
1
1
S2p+1 = 1 + · · · + p + p
+ · · · + p+1 ⇒ S2p+1 −S2p = p
+ · · · + p+1 > p+1 + · · · + p+1
2
2 +1
2 +1
2
2
2
2
|
{z
}
|
{z
}
2p termes
S2p
⇒
S2p+1 − S2p > 2p
1
2p+1
=
1
2
2. La série harmonique alternée :
0
S2p+1 &
1+
⇒
1−
1 1 1
1
+ − + · · · + (−1)n + · · ·
2 3 4
n
S2 S4S6
S2p %
1 1 1
1
+ + + · · · + + · · · = +∞
2 3 4
n
S5S3
1.5
S1
S2p < S2q+1
S2p+1 − S2p → 0
Les sommes partielles ont une limite commune ⇒ la série harmonique alternée converge.
2
Classification des séries
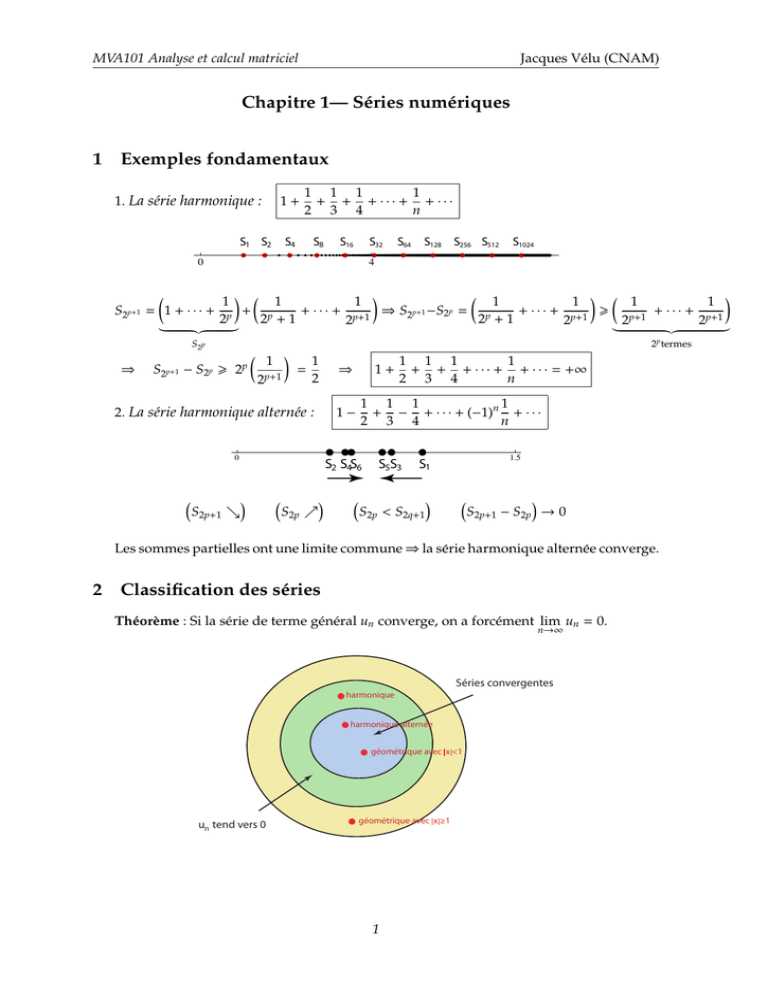
Théorème : Si la série de terme général un converge, on a forcément lim un = 0.
n→∞
Séries convergentes
harmonique
harmonique alternée
géométrique avec x <1
un tend vers 0
géométrique avec x ≥1
1
MVA101 Analyse et calcul matriciel
Jacques Vélu (CNAM)
Séries qui n'ont pas
besoin des signes
Séries qui ont
besoin des signes
harmonique alternée
géométrique avec x <1
Séries à termes
positifs
Séries convergentes
3
Séries à termes positifs
1. Théorème Pour qu’une série à termes positifs converge, il faut et il suffit que les Sn
soient toutes majorées par un même nombre M.
S0
S1 S2 S3
M
On considère deux séries de termes généraux un et vn avec un 6 vn quel que soit n à
partir d’un certain rang. La série de terme général un est la série minorante, la série de terme
général vn est la série majorante.
2. Théorème de comparaison
• Si la série majorante converge, les deux séries convergent.
• Si la série minorante diverge, les deux séries divergent.
3. Règle de d’Alembert
On suppose un > 0 quel que soit n (s’il y a des termes nuls, on les élimine).
un+1
• Convergence s’il existe C < 1 tel que
6 C quel que soit n.
un
un+1
• Divergence si
> 1 quel que soit n.
un
Cas particulier de la Règle de d’Alembert
un+1
= L.
On suppose que lim
n→∞ un
• Si L < 1, la série converge.
• Si L > 1, la série diverge.
4. Règle de Cauchy
On suppose un > 0 quel que soit n.
√
• Convergence s’il existe C < 1 tel que n un 6 C quel que soit n.
√
• Divergence si n un > 1 quel que soit n.
Cas particulier de la Règle
de Cauchy
√
On suppose que lim n un = L .
n→∞
• Si L < 1, la série converge.
• Si L > 1, la série diverge.
2
MVA101 Analyse et calcul matriciel
Jacques Vélu (CNAM)
5. Comparaison avec une intégrale
Soit f une fonction définie sur l’intervalle [1, +∞] , intégrable sur tout intervalle de la
forme [1, A] .
!
Z ∞
Z ∞
Z A
. On dit que
f (t)dt converge si
f (t)dt = lim
f (t)dt existe.
A→∞
1
1
Z1 ∞
. Si la limite n’existe pas, on dit que
f (t)dt diverge.
1
Théorème On suppose f (x) > 0 quel que soit x . Alors
:
Z
∞
La série de terme général un = f (n) et l’intégrale
f (t)dt ont le même comportement.
1
La série de Riemann
4
1+
1
1
1
+ s + · · · + s + · · · converge si et seulement si s > 1.
s
2
3
n
Séries absolument convergentes
1. Théorème Quand la série | u0 | + | u1 | + | u2 | + · · · converge, la série u0 + u1 + u2 + · · ·
converge elle-aussi et :
∞
∞
X
X
un 6
| un |
n=0
n=0
On dit qu’une série convergente u0 + u1 + u2 + · · · est absolument convergente quand la
série | u0 | + | u1 | + | u2 | + · · · converge.
Exemple 1 : Une série géométrique convergente est absolument convergente.
Exemple 2 : La série harmonique alternée n’est pas absolument convergente.
Une série convergente, qui n’est pas absolument convergente, s’appelle une série semiconvergente.
Théorème des séries alternées Soit an une suite de nombres réels positifs qui tend vers
0 en décroissant. Alors la série :
a0 − a1 + a2 − a3 + · · · + (−1)n an + · · ·
converge et les sommes partielles encadrent la somme de la série.
Commentaire : Les séries absolument convergentes sont les « bonnes » séries convergentes.
3