Mathématiques

Commentaires complémentaires sur le programme de cycle 3
Mathématiques
Les nouveaux programmes du cycle 3 mentionnent une initiation à la programmation à travers la
programmation de déplacements ou de construction de figure.
Le collège étant bien doté en matériel informatique pourra prendre cette partie en charge avec
notamment l’utilisation des logiciels scratch et géogébra.
NOMBRES ET CALCULS
 Insister sur l’utilisation de schémas pour la résolution de problèmes.
 Reformuler la règle de multiplication ou de division par 10, 100 ou 1 000.
Souvent on écrit :
« Multiplier un nombre entier par 10 c’est ajouter un zéro. »
« Multiplier un nombre par 10 c’est décaler la virgule d’un rang vers la droite. »
Or ces règles n’ont pas de fondement mathématique et sont source d’erreurs.
Il serait souhaitable d’écrire plutôt :
« Multiplier un nombre par 10 c’est donner à chacun de ses chiffres une valeur 10 fois plus grande. »
Ainsi, on se rend compte que ce n’est pas la virgule qui se déplace mais ce sont les chiffres qui
changent de colonne si on place le nombre dans un tableau de numération.
En parallèle, pour travailler les réflexes, on peut aussi, en calcul mental, donner des calculs du type
« 3 dizaines multipliées par 10 c’est………. »
GRANDEURS ET MESURES
C’est une partie du programme qui pose souvent problème.
Pour les conversions :
Le tableau de conversion est un outil pratique mais son utilisation reste souvent une démarche technique
qui fait oublier le sens de la conversion. Les élèves se trompent déjà au moment de placer le nombre dans
le tableau.
On suggère de ne pas utiliser trop vite un tableau de conversion mais de travailler davantage le sens à
travers le sens des préfixes d’abord. ( kilo veut dire 1 000 fois l’unité……)
Ainsi pour les conversions simples et courantes (de mètres en centimètres, de centimètres en millimètres,
de grammes en kilogrammes…….), les élèves devraient être capables de les faire sans avoir recours au
tableau de conversion. Les règles de numération peuvent être réinvesties.

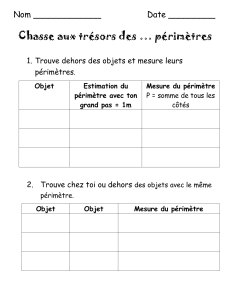
Notion d’aire et périmètre :
Ces notions sont souvent difficiles pour les élèves.
Voici deux résultats statistiques issus d’évaluations nationales
Résultat 1
(EN6/1992 item 118)
Les deux parcelles ont le même périmètre : 32,7 %
Le périmètre de la parcelle B est le plus grand : 46 %
Résultat 2
(EN6/1991 item 109)
Le périmètre de la figure 1 est égal au
périmètre de la figure 2 : 25,6 %
La figure 1 a un périmètre plus grand
que la figure 2 : 57,6 %
Il s’agit d’erreurs fréquentes sur les périmètres mais les erreurs sur les aires sont du même ordre.
Il est donc important d’accorder du temps pour installer ces notions sans avoir recours à des calculs, mais
de travailler la notion de grandeur avant d’introduire une mesure.
On peut comparer des aires ou des périmètres de figures.
On peut aussi modifier une figure, et voir comment varie son aire ou son périmètre.
L’utilisation de formules pour calculer un périmètre n’est pas nécessaire sauf pour la longueur d’un cercle
qui passe maintenant en sixième.
Ne pas introduire de formule d’aire trop vite.
GEOMETRIE
Inciter les élèves à utiliser des figures à main levée.
Distinguer définition et propriétés des figures géométriques.
Définition d’un rectangle : Un rectangle est un quadrilatère ayant quatre angles droits.
Définition d’un losange : Un losange est un quadrilatère ayant quatre côtés de même mesure.
Définition d’un carré : Un carré est un quadrilatère ayant quatre angles droits et quatre côtés de même
mesure.
Un carré est donc un rectangle et un losange à la fois.