Séries entières - pyreach.free.fr

Séries entières
1. Convergence d'une série entière..................................................................................................p.1
Définition d'une série entière d'une variable réelle ou complexe.
Lemme d'Abel. Définition du rayon de convergence d'une série entière. Disque ou intervalle ouvert de convergence.
Critère de comparaison et d'équivalence pour les séries entières. Rayons de convergence de
∑anzn
et
∑n anzn
.
2. Somme d'une série entière d'une variable réelle...................................................................p.6
Fonction somme, domaine de définition.
Continuité de la fonction somme sur l'intervalle ouvert de convergence.
La fonction somme est de classe
C∞
sur l'intervalle ouvert de convergence : dérivation terme à terme.
Intégration terme à terme sur un segment inclus dans l'intervalle ouvert de convergence.
3. Fonctions développables en série entière.................................................................................p.8
Définition d'une fonction développable en série entière au voisinage de 0.
Unicité du développement en série entière.
Développements en série entière usuels :
1
1−x
;
ln ( 1+x )
;
ex
;
( 1+x )
α
;
cos ( x )
;
sin ( x )
Séries de Taylor. Cas des fonctions paires et des fonctions impaires.
4. Exponentielle complexe.................................................................................................................p.13
Expression pour
z∈ℂ
de
ez
sous la forme d'une série entière de variable complexe.
∿∿∿∿∿∿∿∿∿∿∿∿
1. Convergence d'une série entière
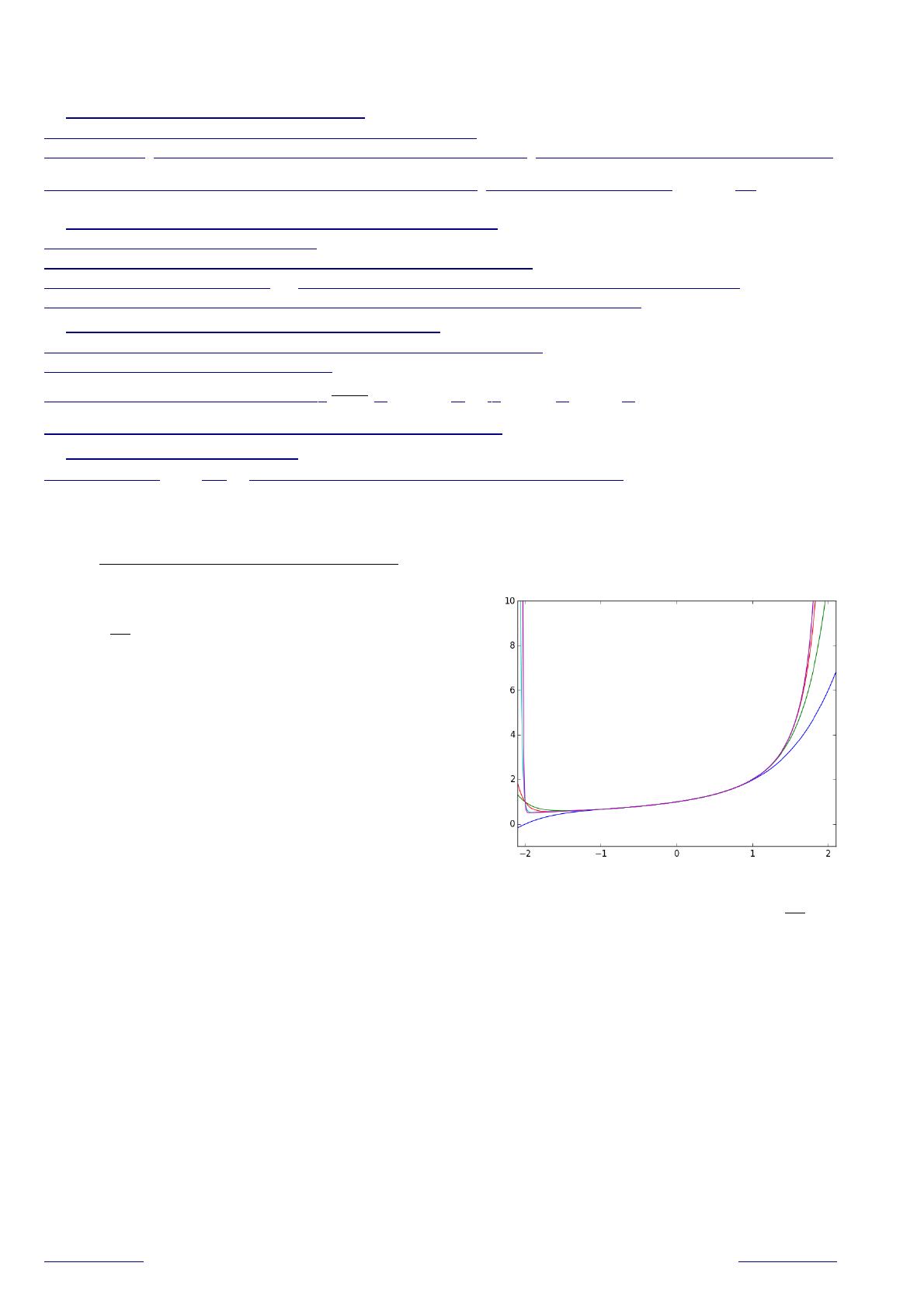
Exemple de code Python permettant de visualiser les
représentations graphiques de fonctions de variable réelle
x→∑
k=0
n1
2kxk
pour différentes valeurs de
n
.
1
2
3
4
5
6
7
8
9
10
11
def S(x,n):
return sum((1/2**k)*x**k for k in range(n+1))
import numpy as np
X=np.linspace(-2.1,2.1,1000)
import matplotlib.pyplot as plt
plt.axis([-2.1,2.1,-1,10])
for k in [5,10,20,100,200]:
Y=[S(x,k) for x in X]
plt.plot(X,Y)
plt.show()
Exemple de code Python permettant de visualiser dans le plan complexe les points d'affixe
z
telle que
∣
∑
k=0
100 1
2kzk
∣
<20
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def S(z,n):
return sum((1/2**k)*complex(z)**k for k in range(n+1))
import numpy as np
Z=[x+y*1j for x in np.linspace(-3,3,100) for y in np.linspace(-3,3,100)]
import matplotlib.pyplot as plt
plt.axis('equal')
for z in Z:
fz=S(z,100)
if abs(fz)<20 :
plt.plot(z.real,z.imag,marker='+')
T=np.linspace(0,2*np.pi,1000)
plt.plot([2*np.cos(t) for t in T],[2*np.sin(t) for t in T],color='black')
plt.show()
Séries entières 1/13 pycreach.free.fr - TSI2

Le critère
∣
∑
k=0
100 1
2kzk
∣
<20
ne prouve en aucun cas la convergence ou la divergence de la série numérique
∑
k⩾0
1
2kzk
Définition d'une série entière d'une variable réelle ou complexe
Soit
(
an
)
une suite de nombres complexes.
Soit
x∈ℝ
, la série de terme général
anxn
, notée
∑anxn
est appelée série entière de variable réelle
x
.
Soit
z∈ℂ
, la série de terme général
anzn
, notée
∑anzn
est appelée série entière de variable complexe
z
.
Rappel :
∀z∈ℂ
,
z0≝1
, ce qui implique en particulier qu'ici
00≝1
.
Remarques : le qualificatif « entière » désigne l'exposant des puissances de
x
ou de
z
.
Les sommes partielles de la série
∑anxn
ou
∑anzn
dépendent ici de la variable complexe
x
ou
z
.
Ainsi pour
n∈ℕ
,
x→∑
k=0
n
akxk
et
z→∑
k=0
n
akzk
sont des fonctions polynomiales définies respectivement sur
ℝ
et
ℂ
.
x→∑
k=0
+∞
akxk
et
z→∑
k=0
+∞
akzk
ne sont pas nécessairement des fonctions polynomiales et leur ensemble de définition
n'est pas nécessairement
ℝ
et
ℂ
.
Remarque : Une série de type
∑bnz2n
par exemple, est appelée série lacunaire car …
Exemples : si pour tout entier naturel
n
,
an=
(
−1
)
n
alors la série entière
∑anzn
est la suite des sommes partielles :
S0 ( z ) =…
S1 ( z ) =…
S2 ( z ) =…
Si
∣ z ∣ <1
alors
∑
k=0
+∞
( −1 )
kzk
=...
Lemme d'Abel : condition suffisante de convergence d'une série entière sur un disque ouvert
Soit
(
an
)
une suite de nombres complexes et un réel
r>0
.
Si la suite
(
anrn
)
n∈ℕ
est bornée alors
∀z∈ℂ
tel que
∣ z ∣ <r
, la série
∑anzn
est absolument convergente.
Démonstration : Soit un réel
M>0
tel que
∀n∈ℕ
,
∣
an
∣
(
r
)
n⩽M
Par ailleurs,
∀z∈ℂ
,
∣
anzn
∣
=
∣
an
∣
∣
z
∣
n=
∣
an
∣
(
r
)
n
(
∣
z
∣
r
)
n
⩽M
(
∣
z
∣
r
)
n
Ainsi, si
∣ z ∣ <r
alors
0⩽
∣ z ∣
r<1
donc la série numérique
∑M
(
∣
z
∣
r
)
n
est une série géométrique convergente.
Séries entières 2/13 pycreach.free.fr - TSI2

Ainsi, d'après le critère de majoration pour les séries à termes positifs, la série
∑
∣ anzn ∣
est convergente. □
Remarque : l'ensemble I=
{
r∈ℝ+∣la suite
(
anrn
)
est bornée
}
est un intervalle du type
[ 0;R [
ou
[ 0;R ]
.
En effet, si
r0∈I
alors
( ∣
an
∣
rn
)
est bornée, donc
∀r∈
[
0;r0
]
, la suite
( ∣
an
∣
rn
)
est bornée, ainsi
[
0;r0
]
⊂I
.
Cette propriété de connexité caractérise les intervalles de
ℝ
.
Définition du rayon de convergence d'une série entière
Soit
∑anzn
une série entière.
Le rayon de convergence de cette série est :
R≝sup
{
r∈ℝ+ ∣la suite
(
anrn
)
est bornée
}
.
Remarque : le rayon de convergence est une borne supérieure d'un intervalle de
ℝ+
donc le rayon de convergence d'une
série entière peut être un réel positif ou
+∞
.
Théorème sur la nature d'une série entière d'une variable complexe
Soient
∑anzn
une série entière et R son rayon de convergence.
►
∀z∈ℂ
tel que
∣ z ∣ <R
, la série
∑anzn
est absolument convergente.
►
∀z∈ℂ
tel que
∣ z ∣ >R
, la série
∑anzn
est grossièrement divergente car la suite
(
anzn
)
n'est pas bornée.
Démonstration :
1) Si
∣ z ∣ <R
alors il existe
r∈ ] ∣ z ∣ ;R [
donc, par définition de R la suite
(
anrn
)
est bornée, ainsi, d'après le lemme d'Abel,
la série
∑anzn
converge absolument.
2) Si
∣ z ∣ >R
, supposons par l'absurde que la suite
(
anzn
)
soit bornée.
Alors en posant
r= ∣ z ∣
, on a
(
anrn
)
bornée et
r>R
ce qui contredit la définition de R.
La suite
(
anzn
)
n'est pas bornée donc pas convergente, la série
∑anzn
est donc grossièrement divergente. □
Pour
∣ z ∣ =R
la série
∑anzn
peut être absolument convergente, convergente ou divergente.
Définitions du disque ouvert de convergence et de l'intervalle ouvert de convergence
Soient
∑anzn
une série entière de variable complexe et R son rayon de convergence. Le disque ouvert de centre 0 et
de rayon R, noté
D≝ { z∈ℂ∣ ∣ z ∣ <R }
, est appelée disque ouvert de convergence de
∑anzn
.
L'application :
D→ ℂ
z→∑
n=0
+∞
anzn
est appelée fonction somme de
∑anzn
.
Soient
∑anxn
une série entière de variable réelle et R son rayon de convergence. L'intervalle
] −R ; R [
est appelé
intervalle ouvert de convergence de
∑anxn
L'application :
] −R ; R [ → ℝ
x→∑
n=0
+∞
anxn
est appelée fonction somme de la série entière
∑anxn
.
Séries entières 3/13 pycreach.free.fr - TSI2

Remarque : si R=0 alors ...
Si
R=+∞
alors...
Remarque : le rayon de convergence peut être
défini de façon analogue par :
R=sup
{
r∈ℝ+∣la série ∑anrn converge
}
L'ensemble de définition de la fonction somme
peut être étendu aux points du cercle d'incertitude
pour lesquels la série
∑anzn
converge.
Méthodes utilisant les séries numériques pour déterminer le rayon de convergence
Soit R le rayon de convergence de la série entière
∑anzn
et
z0∈ℂ
.
► Si la série numérique
∑an
(
z0
)
n
est absolument convergente alors
R⩾
∣
z0
∣
► Si la série numérique
∑an
(
z0
)
n
est convergente mais pas absolument convergente alors
R=
∣
z0
∣
► Si la série numérique
∑an
(
z0
)
n
est grossièrement divergente alors
R⩽
∣
z0
∣
► Si (la série numérique
∑anzn
converge si et seulement si
∣ z ∣ ⩽
∣
z0
∣
) alors
R=
∣
z0
∣
► Si (la série numérique
∑anzn
converge si et seulement si
∣ z ∣ <
∣
z0
∣
) alors
R=
∣
z0
∣
Exemple : pour la série
∑
n⩾1
1
nzn
on a : pour
r=1
...
Et pour
r=−1
… Donc...
Critères d'équivalence ou de comparaison des modules des termes généraux
Soient
∑anzn
et
∑bnzn
deux séries entières de rayons de convergence respectifs
Ra
et
Rb
:
► critère d'équivalence : si
∣
an
∣
∼
+∞
∣
bn
∣
alors
Ra=Rb
► critère de comparaison : si
∀n∈ℕ
,
∣
an
∣
⩽
∣
bn
∣
alors
Ra⩾Rb
Démonstration : ► Si
∣
an
∣
∼
+∞
∣
bn
∣
alors pour tout réel
r>0
,
∣
an
∣
rn∼
n→+∞
∣
bn
∣
rn
Ainsi :
(
anrn
)
est bornée si et seulement si
(
bnrn
)
est bornée
Donc
{
r∈ℝ+∣la suite
(
anrn
)
est bornée
}
=
{
r∈ℝ+∣la suite
(
bnrn
)
est bornée
}
, donc
Ra=Rb
.
► Si
∀n∈ℕ
,
∣
an
∣
⩽
∣
bn
∣
alors pour tout réel
r>0
,
∣
an
∣
rn⩽
∣
bn
∣
rn
Ainsi : Si la suite
(
bnrn
)
est bornée alors la suite
(
anrn
)
est bornée
Donc :
{
r∈ℝ+∣la suite
(
bnrn
)
est bornée
}
⊂
{
r∈ℝ+∣la suite
(
anrn
)
est bornée
}
Ainsi :
Rb⩽Ra
□
Remarque : il suffit que
∣
an
∣
⩽
∣
bn
∣
soit vérifiée à partir d'un certain rang pour pouvoir affirmer
Ra⩾Rb
.
Propriété de conservation du rayon de convergence par multiplication du terme général par
n
Les séries entières
∑anzn
et
∑n anzn
ont même rayon de convergence.
Remarque : en utilisant cette propriété, on peut démontrer par le critère d'équivalence puis par récurrence que, quelle que
Séries entières 4/13 pycreach.free.fr - TSI2

soit le polynôme P ou la fraction rationnelle Q, les séries entières
∑P
(
n
)
anzn
et
∑Q
(
n
)
anzn
ont le même rayon de
convergence que celui de la série entière
∑anzn
.
Démonstration : Soit R et R' les rayons de convergence des séries entières
∑anzn
et
∑nanzn
.
∀n∈ℕ
*,
1⩽n
donc
∣
an
∣
⩽n
∣
an
∣
donc, d'après le critère de comparaison,
R⩾R'
.
Supposons, par l'absurde,
R>R'
alors il existe
r∈ℝ
et
z0∈ℂ
tels que :
R'<
∣
z0
∣
<r<R
{
R'<
∣
z0
∣
⇒la suite
(
nan
(
z0
)
n
)
est non bornée
r<R⇒la suite
(
anrn
)
est bornée par M>0
Or
n
∣
an
(
z0
)
n
∣
=n
∣
an
∣
(
∣
z0
∣
n
rn
)
rn=
( ∣
an
∣
rn
)
(
n
(
∣
z0
∣
r
)
n
)
⩽Mn
(
∣
z0
∣
r
)
n
or
0⩽
∣
z0
∣
r<1
donc en posant
q=
∣
z0
∣
r
, on a :
n qn=eln
( n ) +nln ( q )
avec
ln ( q ) <0
En vertu des croissances comparées,
lim
n→+∞
ln ( n ) +nln ( q ) =−∞
donc par composition
lim
n→+∞
n qn=0
.
Ainsi par application du théorème d'encadrement
lim
n→+∞
n ∣ an
(
z0
)
n
∣ =0
ce qui contredit le fait que la suite
( n a n
(
z0
)
n
)
soit
bornée. □
Remarque : la série
∑
n⩾1
nanzn−1=∑
(
n+1
)
an+1zn
est appelée dérivée formelle de la série entière
∑anzn
.
Exemple : pour la série
∑n2nz2n
…
Méthode : détermination du rayon de convergence à l'aide de la règle de d'Alembert
Soient
∑anzn
une série entière telle que
∀n∈ℕ
,
an≠0
et R son rayon de convergence.
Soit un réel
r>0
, la règle de d'Alembert appliqué à la série
∑
∣
an
∣
rn
considère le quotient :
∣
an+1
∣
rn+1
∣
an
∣
rn=r×
∣
an+1
an
∣
► Si
lim
n→+∞
∣
an+1
an
∣
=L≠0
alors
lim
n→+∞
∣
an+1
∣
rn+1
∣
an
∣
rn=r×L
Ainsi,
∀r∈
]
0 ; 1
L
[
,
r×L<1
donc, d'après la règle de d'Alembert pour les séries à termes positifs, la série
∑
∣
an
∣
rn
converge.
En revanche,
∀r∈
]
1
L;+∞
[
,
r×L>1
donc, d'après la règle de d'Alembert pour les séries à termes positifs, la série
∑
∣
an
∣
rn
diverge.
Conclusion :
R=1
L
.
► Si
lim
n→+∞
∣
an+1
an
∣
=0
alors
∀r>0
,
lim
n→+∞
∣
an+1
∣
rn+1
∣
an
∣
rn=r×0=0<1
donc, d'après la règle de d'Alembert pour les séries à
termes positifs, la série
∑
∣
an
∣
rn
converge. Ce raisonnement étant valide pour tout réel
r
positif,
R=+∞
.
► Si
lim
n→+∞
∣
an+1
an
∣
=+∞
alors
∀r>0
,
lim
n→+∞
∣
an+1
∣
rn+1
∣
an
∣
rn=+∞
donc, d'après la règle de d'Alembert pour les séries à
termes positifs, la série
∑
∣
an
∣
rn
diverge. Ce raisonnement étant valide pour tout réel
r
positif, on a
R=0
.
Exemples :
∑1
n!zn
... et
∑nn
n!zn
...
Séries entières 5/13 pycreach.free.fr - TSI2