1. Les différents outils à utiliser au cycle 3

1
1. LES DIFFERENTS OUTILS A UTILISER AU CYCLE 3
a- La règle non graduée et le compas :
- La règle non graduée permet de tracer des droites passant par deux
points, de vérifier l’alignement de trois points ou plus, de tracer un
segment de droite d’extrémités connues.
La règle peut aussi être une bande de papier dont on se sert pour
reporter une longueur d’un segment sur un autre (il suffit d’y faire
une marque ou de le couper au bon endroit).
- On peut se servir d’un compas à pointe sèche pour reporter ou
comparer des longueurs. Mais le compas sert d’abord à tracer des
cercles et des arcs de cercle de centre et de rayon donnés. Comme
pour le tracé d’un segment avec la règle, la coordination des gestes de
maniement du compas n’est pas une simple formalité pour beaucoup
d’enfants, même au cycle 3.
b- La règle graduée, l’équerre et le gabarit
- La règle graduée permet en outre de tracer un segment de longueur
connue, ou de mesurer la longueur d’un segment déjà dessiné.
- L’équerre sert à tracer des angles droits et des droites
perpendiculaires. En la faisant glisser sur une règle, on s’en sert aussi
pour dessiner des droites parallèles. Avec l’équerre, on peut donc
contrôler qu’un angle est droit, que deux droites sont
perpendiculaires ou parallèles.
- On peut fabriquer une équerre en pliant deux fois une feuille de
papier (le deuxième pli doit se retrouver sur le premier : on a ainsi
fabriqué un gabarit d’équerre).
- On peut enfin utiliser des gabarits pour compléter des tracés ou pour
contrôler des angles.
c- Pourquoi utiliser la règle et le compas ?
1
Les mathématiciens grecs se sont intéressés à la règle et le compas mais très tôt ils se
sont heurtés à de grandes difficultés.
Dès le cinquième siècle avant J.C. sont apparus des problèmes que l’on n’arrivait pas à
résoudre à la règle et au compas. Ces problèmes ne tardèrent pas à devenir célèbres après les
échecs de mathématiciens réputés.
Trop confiants dans la règle et le compas, qui dans d’autres constructions leur avaient
fourni des solutions élégantes, les mathématiciens grecs n’ont jamais envisagé l’impossibilité
des constructions demandées, il en sera d’ailleurs de même pour leurs successeurs.
les raisons qui ont conduit les mathématiciens grecs à privilégier dans leurs études la
règle et le compas.
 La première raison que l’on peut évoquer est une raison élémentaire.
Les courbes les plus simples qui interviennent en géométrie sont la
droite et le cercle et les instruments les plus simples pour les construire
sont la règle et le compas. Cette raison de bon sens permet de
comprendre pourquoi les grecs ont considéré les constructions à la règle
1
Théorie des corps, la règle et le compas - J.C. CARREGA – Ellipses.

2
et au compas mais elle ne permet pas d’expliquer pourquoi ils y étaient
attachés si profondément.
 Il faut aussi évoquer, au quatrième siècle avant J.C., l’influence de
Platon (423-348) et de son école, l’Académie. Pour Platon, le cercle que
l’on trace ne représente qu’imparfaitement le cercle idéal (c’est celui
qui répond à la définition du cercle, c’est lui que le mathématicien
prend pour objet de sa spéculation). Les figures ne sont donc qu’un pâle
reflet de la réalité, qui, elle, appartient au monde des idées. Ces
conceptions amènent Platon à avoir peu d’estime pour les instruments
de mesure ou de construction nécessairement imparfaits. Il fait toutefois
une exception pour la règle et le compas qui sont les seuls, à ses yeux, à
pouvoir respecter la symétrie des configurations.
 Pour convaincre, une démonstration devait être accompagnée d’une
figure claire effectuée à l’aide d’instruments simples connus et admis
par tous. Cette troisième raison évoque donc la faiblesse des
démonstrations de l’époque.
 Enfin, on peut penser, mais ceci n’est qu’une hypothèse, que les
constructions à la règle et au compas ont été mises en avant pour servir
de caution géométrique aux nouveaux nombres mis en évidence par le
théorème de Pythagore. De plus, en s’interdisant d’autres types de
constructions on se préservait contre de nouvelles crises.
2. LES CONSTRUCTIONS ELEMENTAIRES AU CYCLE 3
a- Les figures
1- Le parallélogramme quelconque ou non particulier
Côtés
Angles
Diagonales
côtés opposés
égaux et
parallèles.
angles opposés
égaux.
se coupent en
leur milieu.
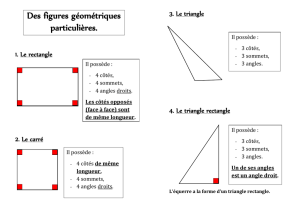
2- Le rectangle
Côtés
Angles
Diagonales
Symétrie

3
côtés
opposés
égaux et
parallèles
4 angles
droits
- d’égale
longueur
- se coupent en
leur milieu
2 axes de
symétrie
3- Le carré
Côtés
Angles
Diagonales
Symétrie
- 4 côtés égaux
- côtés opposés
parallèles.
4 angles
droits.
- d’égale longueur
- se coupent en
leur milieu et sont
perpendiculaires.
4 axes de
symétrie.
4- Le losange
Côtés
Angles
Diagonales
Symétrie
- 4 côtés égaux
- côtés opposés
parallèles.
angles
opposés
égaux.
se coupent en
leur milieu et
sont
perpendiculaires
.
2 axes de
symétrie.

4
5- Le triangle isocèle
Côtés
Angles
Symétrie
2 côtés égaux.
2 angles
égaux.
1 axe de
symétrie.
6- Le triangle équilatéral
Côtés
Angles
Symétrie
3 côtés
égaux
3 angles égaux
à 60°
3 axes de
symétrie
b- Les droites
1- Les parallèles
Deux droites sont parallèles si elles sont confondues ou si elles n’ont aucun point
commun et s’il y a un ”écartement constant” entre elles deux.

5
On note que : (d) // (d’).
Méthode de tracé d’une droite parallèle à une droite (d) passant par A en utilisant l’équerre :
A
2- Les perpendiculaires (médiatrice et hauteur) :
 Définition
Deux droites sont perpendiculaires si elles se coupent en formant un angle droit.
On note que : (d) ┴ (d’).
Si deux droites sont perpendiculaires, elles
déterminent alors quatre angles droits.
1- Méthode de tracé de la perpendiculaire à (d) passant par A en utilisant l’équerre et la règle :
A
(d)
Equerre
2
(d)
(d’)
(d)
(d’)
(d)
(d)
(d’)
1- On trace une perpendiculaire à (d).
2- Puis, on trace la perpendiculaire passant
par A à la perpendiculaire que l’on vient
de tracer.
1
Règle
On place la règle le long de la droite
(d), puis, on fait glisser l’équerre sur
cette même règle jusqu’au point A.