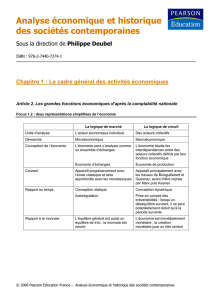
Þ i

Ecole supérieure de commerce
Cours de macroéconomie
Première année Master
Document d’appui au cours
Préparé par
Pr ILMANE Mohamed-Chérif
Décembre 2011

Avant propos
Ce document comprend deux parties : une parie théorique et une partie appliquée.
La partie théorique consiste en un exposé concis sur l’équilibre macroéconomique.
L’exposé débute par l’étude des agrégats macroéconomiques à travers les principales
opérations (sur biens et services, financières et en capital) et les comptes des agents
économiques. Ces opérations sont ensuite traduites en termes de circuit macroéconomique
afin de visualiser les interdépendances entre agents économiques.
Après cette étude de nature comptable, vient l’exposé de la théorie économique : c’est-à-dire
l’étude des comportements des différents agents économiques.
L’approche privilégiée est l’approche keynésienne suivant le modèle IS–LM.
La démarche pédagogique adoptée consiste à évoluer étape par étape du plus simple : une
économie fermée, sans Etat et des prix constants, au plus complexe : introduction de l’agent
Etat via la politique économique, ouverture de l’économie aux échanges avec le reste du
monde, variation des prix, taux de change,…
La partie appliquée porte sur l’analyse de la réalité algérienne. Il s’agit plus précisément
d’un exposé sur l’équilibre ressources emplois. Un exemple détaillé pour l’année 2005 a été
fourni afin de permettre aux candidats de tester leurs connaissances, il est mis à leur
disposition la batterie complète de données relatives à la période 2006 -2010.

I – Agents et agrégats macroéconomiques
I – 1 – Opérations (sur biens et services, financières et en capital) et comptes d’agents
Opérations et comptes d’agents
Emplois Entreprises Ressources
Emplois Ménages Ressources
Emplois Système bancaire Ressources
Emplois Administrations Ressources
Emplois Reste du monde Ressources
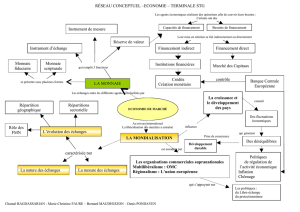
I – 2 – Circuit macroéconomique : flux monétaires et financiers
Salaires………………………W
Taxes et Impôts……………...Te
Dividendes…………………Dm
Intérêts versés……………...Rbe
Epargne :…………………….Se
Investissements……………...I
Monnaie………………....∆Me
Production (VA) : ………………Y
Epargne :……………………….Se
Crédits bancaires :………… ..∆Cre
Titres :……………………….∆Be
Consommation : ………………..C
Impôts et taxes :……………….Tm
Intérêt payés :………………..Rbm
Epargne………………………..Sm
Titres :………………………∆Bm
Monnaie :……………… …∆Mm
Salaires :………………………..W
Traitements :……………………Tr
Dividendes :……………… ….Dm
Epargne :………………………Sm
Crédits :…………………….∆Crm
Intérêts reçus :………Re + Rm = Rb
Epargne………………………….Sb
Monnaie :………∆Me + ∆Mm = ∆M
Réserves de change :…………∆FA
Crédits :…∆Cre+∆Crm+∆Crg = ∆Cr
Titres :………………………….∆Bb
Dépenses publiques :……………G
Epargne :……………………….Sg
Impôts et Taxes :…….Te+Tm = T
Epargne……………………….Sg
Titres :……………………….∆Bt
Crédits/ avances…………∆Crg
Importations B&S :…………….IM
Excédent courant……………….Exc
Compte capital…………………∆Bk
Réserves de change :…………..∆FA
Exportations B&S :……………...EX
Excédent courant………………..Exc

E
N
T
R
E
P
R
I
S
E
S
M
E
N
A
G
E
S
INSTITUTIONS FINANCIERES
ETAT
RESTE
DU
MONDE
Marché
Financier
Marché
Monétaire
Marché du
Crédit
BIENS
&
SERVICES
C
I
EX
IM
Y
Te
Tm
G
W+ DIVID.
∆Bg
∆Bm
∆Be
∆Cre
∆Crm
∆Me
∆Mm
Re
∆FA (-)
∆FA (+)
∆Cr
∆M
∆Crg
∆Bb
Trait.
CIRCUIT MACROECONOMIQUE : flux monétaires et financiers

II – De la comptabilité aux comportements
Contrairement au comptable qui raisonne ex post, l’économiste raisonne ex ante. Le comptable
travaille sur les données ou les faits réalisés. L’économiste travaille sur les mécanismes
d’ajustement des différentes variables économiques en recherchant les causes qui conduisent
aux résultats comptables. Pour cela, l’économiste considère les comportements des agents
économiques.
Mais alors que le comptable est exhaustif, l’économiste raisonne généralement en termes de
moyenne. Aussi, n’étant pas en mesure, voire qu’il n’est pas nécessaire, de capter la réalité dans
tous ses détails, l’économiste, en scientifique, recourt à la simplification, à l’abstraction : il
élabore une théorie. Pour revenir à la réalité et en faire l’analyse, l’économiste recourt à un
instrument opérationnel : le modèle.
L’élaboration d’une théorie et donc la construction d’un modèle, consiste à faire des
hypothèses sur les comportements des agents économiques.
Pour que le modèle soit le plus réaliste possible, il faut que les hypothèses sur lesquelles est
assis reflètent le mieux possible les comportements en question. Il est évident que plus les
hypothèses sont réalistes, c’est-à-dire plus on se rapproche de la réalité, plus le modèle devient
complexe. Il vient un moment où la complexification ne servirait à rien, car elle n’apporte pas,
ou pas suffisamment, d’informations supplémentaires qui amélioreraient de manière
pertinente la compréhension du phénomène étudié. Il n’est donc pas utile de compliquer le
modèle si le coût de cette complexification est supérieur au gain en informations qu’elle
permet.
Sur le plan pédagogique, il est impératif d’aborder le problème de manière la plus simple
possible, c’est-à-dire la plus abstraite possible, pour repérer, isoler le mécanisme de base. Il
s’agira, ensuite, d’accroître la complexité en procédant au "relâchement" des hypothèses.
A propos du sujet qui nous réunis ici : l’analyse macroéconomique, nous procéderons de la
manière suivante :
1. nous considérerons d’abord une économie fermée et sans l’agent Etat ;
2. nous introduirons ensuite l’Etat, tout en gardant l’hypothèse d’économie fermée ;
3. enfin, nous intégrerons les relations économiques avec le reste du monde.
Outre ces hypothèses d’ordre plutôt pédagogique, nous supposerons que les prix demeureront
constants. Cette hypothèse forte peut se justifier car nous raisonnerons dans l’hypothèse du
court terme. Nous y reviendrons lorsque nous aurons levé toutes les hypothèses simplificatrices.
Après l’exposé théorique soutenu par des exercices fictifs pour fixer les idées, nous
procéderons à une application au cas algérien. Cette application portera sur l’équilibre
macroéconomique pour les années 2004 – 2007 et les politiques monétaire et budgétaire durant
les mêmes années. La discussion sera précédée par un exposé succinct sur l’évolution
macroéconomique 1990-2006, en mettant l’accent sur la période de stabilisation 1994-1998.
Aussi, un exposé concis sera consacré au taux de change du DA.