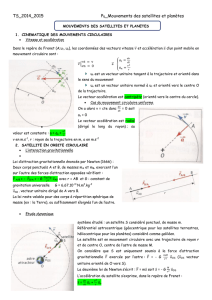
Mouvement des satellites et des planètes

1
Mouvement des satellites et des planètes.
Introduction.
On appliquera ici la 2ème loi de Newton à l’étude du mouvement de corps astronomiques : les
satellites et les planètes.
I. Aspect historique : les lois de Kepler.
1. Introduction.
En rassemblant et complétant l’ensemble des observations astronomiques effectuées par les
astronomes jusqu'à son époque, Kepler a réussi, uniquement à partir de données
expérimentales (démarche heuristique), a dégagé trois lois fondamentales régissant le
mouvement des planètes autour du soleil.
Ces lois permettront à Newton quelques décennies plus tard de déterminer l’expression de la
loi de gravitation universelle.
2. Le référentiel héliocentrique.
Le mouvement des planètes du système solaire est étudié dans le référentiel héliocentrique
(« centré sur le soleil »).
Ce référentiel est défini par le centre du soleil et par trois axes dirigés vers des étoiles
lointaines.
Le référentiel héliocentrique est un référentiel galiléen.
3. Les lois de Kepler.
Les lois de Kepler sont énoncées dans le référentiel héliocentrique.
Etoile α
Soleil
Etoile β
Etoile γ

2
3.a. 1ère loi : loi des orbites.
Toutes les planètes ont une orbite elliptique ; le soleil étant situé à l’un des foyers de
cette ellipse.
Eléments mathématiques :
Une ellipse de foyers F1 et F2 est constituée par l’ensemble des points M tels que
F1M + F2M = constante.
r1 + r2 = constante
a est la longueur du demi grand axe, b est la longueur du demi petit axe.
On a donc la trajectoire :
3.b. 2ème loi : loi des aires.
Au cours du mouvement d’une planète sur son orbite, l’aire (la surface) balayée par le
segment reliant le soleil à la planète pendant un intervalle de temps Δt donné reste
constante.
●
F1
●
F2
r1
r2
M
●
a
b
●
F1
●
F2
soleil
planète

3
S1 = S2
Il en résulte que la vitesse de la planète est d’autant plus importante qu’elle se trouve
près du Soleil.
3.c. 3ème loi : loi des périodes.
Soit T la période de révolution d’une planète autour du soleil (T est le temps que met la
planète pour faire « un tour complet »), soit a la longueur du demi grand axe de la
trajectoire elliptique de la planète, on constate que le rapport
3
2
a
T
a une valeur
identique pour toutes les planètes du système solaire.
On se propose dans la suite de ce cours d’étudier le mouvement des satellites terrestre et des
planètes en utilisant la 2ème loi de Newton et de retrouver ainsi, au moins partiellement, les
lois de Kepler.
II. Etude du mouvement des satellites terrestres.
1. Le référentiel géocentrique.
Le référentiel terrestre ne peut être considéré comme galiléen dans l’étude du mouvement des
satellites (sinon un satellite géostationnaire, immobile au dessus d’un point de la surface
terrestre, devrait tomber en chute verticale !).
Le référentiel adapté à cette étude est le référentiel géocentrique, qui peut être considéré
comme galiléen lors de l’étude du mouvement des satellites terrestres.
Le référentiel géocentrique est défini par le centre de la terre et par trois axes parallèles à ceux
du référentiel héliocentrique.
Dans le référentiel géocentrique, la terre a un mouvement de rotation autour de son axe
Nord-Sud avec une période de rotation de 24 heures (23 h 56 min).
2. La force de gravitation.
Un satellite terrestre est uniquement soumis à la force d’attraction gravitationnelle de la terre
(on néglige l’attraction du soleil, de la lune et des autres satellites).
Δt
Δt
S1
S2

4
Si on considère que la terre a une répartition sphérique de masse et que le satellite est de petite
dimension par rapport à la distance qui le sépare du centre de la terre, la loi de gravitation
universelle permet de connaître les caractéristiques de cette force
F
:
- Point d’application : centre d’inertie du satellite.
- Direction : droite centre de la terre – centre d’inertie du satellite
- Sens : vers le centre de la terre (attraction)
- Intensité :
F =
2
r
MmG T
G est la constante de gravitation universelle ; G = 6,67 10-11 SI
m est la masse du satellite
MT la masse de la terre
R la distance du satellite au centre de la terre.
On peut donner une expression vectorielle de cette force en définissant un vecteur unitaire
u
orienté du centre de la terre vers le satellite (voir figure) ; on a alors :
F
=
2
r
MmG T
u
Le signe « moins » rappelle le caractère attractif de la force de gravitation.
3. Application de la 2ème loi de Newton.
On applique la 2ème loi de Newton au système {satellite}dans le référentiel géocentrique
considéré comme galiléen ; le satellite étant uniquement soumis à la force d’attraction
terrestre, on a :
m
G
a
=
F
=
2
r
MmG T
u
Soit :
G
a
=
2
r
MG T
u
relation 1
- L’accélération du satellite est indépendante de sa masse ; le mouvement du satellite
est donc indépendant de sa masse.
u
F
Terre
●
Satellite
r

5
- Le vecteur
G
a
est constamment dirigé vers le centre de la terre : l’accélération est
centripète.
Trouver les caractéristiques du mouvement du satellite (équations horaires, trajectoire,…) à
partir de la relation 1 nécessite dans le cas général un traitement mathématique relativement
complexe, le vecteur accélération
G
a
variant à la fois en direction (
u
varie) et en norme (r
varie) en fonction du temps (une telle étude permet de retrouver les lois de Kepler).
On s’intéressera uniquement ici au cas particulier important où le mouvement du satellite est
circulaire uniforme, après avoir défini les outils mathématiques bien adapté à l’étude d’un
mouvement circulaire.
4. Etude du mouvement circulaire.
On considère un mobile ponctuel M en mouvement circulaire, sa trajectoire étant un cercle de
centre O et de rayon R.
L’emploi d’un repère orthonormée est généralement mal adapté à l’étude d’un mouvement
circulaire, le vecteur accélération n’étant, dans le cas général, ni constant en direction ni
constant en norme.
On utilise alors un repère lié au mobile M, appelé repère de Frenet.
Le repère de Frenet est défini par deux vecteurs unitaire (
T
,
N
) lié au point M, le vecteur
T
,
appelé vecteur tangent, étant tangent au cercle trajectoire au point M et le vecteur
N
, appelé
vecteur normal, étant dirigé vers le centre O du cercle.
Dans le repère de Frenet le vecteur vitesse s’exprime sous la forme :
v
= v
T
, ou v est la
norme du vecteur vitesse.
On montre par ailleurs que le vecteur accélération du mobile M a pour expression :
a
=
dt
dv
T
+
R
v2
N
●
O
Sens du
mouvement
●M
T
N