Equation Section 1

Equation Section 1
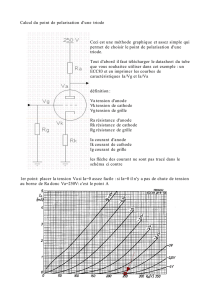
La diode à vide, un conducteur non-ohmique
Les deux électrodes A et C d’une diode sont enfermées dans une ampoule où règne le vide. La
cathode C émet, par effet thermoélectrique, des électrons sans vitesse initiale qui sont attirés par
l’anode A maintenue au potentiel V0 constant et positif (Figure 1).
Figure 1
En régime permanent, les électrons, de charge – e et de masse m, quittent la cathode qui se situe
dans le plan x = 0 ; ils se dirigent vers l’anode positionnée au plan x = L.
a) Quelle est la géométrie des équipotentielles ?
b) Ecrire les 3 équations locales uni-dimensionnelles qui relient le potentiel Vx, la vitesse vx des
électrons émis et le nombre d’électrons nx par unité de volume en un point M situé à la
distance x de la cathode (0 < x < L).
c) Présenter l’équation différentielle du potentiel Vx.
d) L’expérience confirme qu’un nuage de conduction existe entre la cathode et l’anode ; calculer
le potentiel Vx entre ces deux plans.
e) En déduire une expression de la densité de courant ja sur l’anode.
f) En rappelant la définition du flux de ja, trouver une expression du courant d’anode Ia en
fonction des données et du potentiel d’anode Va.
Corrigé
a) En première approximation, les équipotentielles sont des plans perpendiculaires à l’axe Ox. Les
lignes de champ
E
sont parallèles à l’axe Ox près de celui-ci et à peu près parallèles loin de celui-
ci mais toujours entre la cathode et l’anode.
b) Le théorème de l’énergie cinétique, appliqué à l’électron émis entre la cathode et le point P,
s’écrit :
2
1
2m v x eV x
Donc :
2e
v x V x
m
(1.1)
Remarque :On aurait pu penser à appliquer le principe fondamental de la dynamique (2e loi de
Newton) mais l’équation obtenue donne la vitesse en fonction du temps (vitesse croissant
linéairement), et ce n’est pas la dépendance que nous cherchons.
O
L
x
cathode
anode
Vc = 0
Va
P

L’équation de Poisson s’écrit en P :
0
0
x
Vx
, où la densité volumique de charge est
x eN x
.
Donc :
2
20
d V x eN x
dx
(1.2)
a
j eN x v x  
a
j
N x v x e
(1.3)
c) Eliminons v(x) et N(x) entre les équations (1.1), (1.2) et (1.3) ; d’après (1.2) et (1.3), on a :
2
20
1
a
d V x j
dx v x
et d’après (1.1),
2
202
a
d V x jm
dx eV x
d) Cette équation différentielle est de la forme :
212
2
dV kV
dx 
avec
02
a
jm
ke
(1.4)
Pour résoudre cette équation différentielle en V(x), multiplions les deux membres de cette équation
par 2 dV/dx, soit :
212
2
22 dV d V dV
kV
dx dx dx
En intégrant, il vient :
212
4
dV kV cte
dx
Remarque : Avant d’intégrer, on peut légitimement se poser la question : est-ce que ja est indépendant
de x ? En effet, l’équation (1.3) laisse supposer que ja dépend de x et que l’intégration va s’avérer
impossible. Il faut s’imaginer la diode en régime permanent, un courant d’intensité constante la
traverse. Cette intensité est égale au flux de ja à travers la surface des électrodes. Cette surface est
bien entendu constante, par conséquent, ja est une constante sur tout le trajet des électrons entre la
cathode et l’anode. Au niveau de la cathode, les électrons ont une vitesse extrêmement faible et la
densité volumique est importante (ça embouteille dur !), mais au fur et à mesure que les électrons
prennent de la vitesse, le « trafic se fluidifie », la densité volumique diminue, de sorte que le produit
N x v x cte
.
Au niveau de la cathode (x = 0), on a V = 0 et
0
dV
Edx
, donc cte = 0 ; on en déduit :
14
2
dV kV
dx 
Séparons les variables :
14 2V dV k dx
et intégrons :
34 3 4 2V k x cte  
, la constante est nulle car V = 0 pour x = 0.

Le potentiel électrostatique en P obéit donc à la loi :
43 23
4 3 4 3
39
24
k
V x x k x
,
Soit, d’après (1.4) :
23
43
0
9
42
a
jm
V x x
e
L’hypothèse E = 0 en C signifie qu’au niveau de la cathode, le champ dû aux charges des électrodes
est égal et opposé au champ dû aux charges d’espace.
e)
32
02
421
9
ae
j V x
mx
32
02
421
9
a
S
e
I j ds V L S
mL
, avec
A
V L V
, on obtient :
32
A
I K V
avec
02
42
9Se
KLm