Reconnaissance des lois usuelles

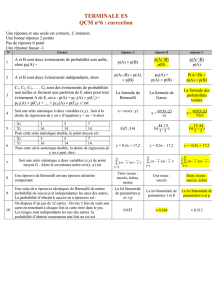
RECONNAISSANCE DES LOIS USUELLES
RETOUR AU MENU VARIABLES DISCRETES
RETOUR ACCUEIL
Remarque méthodologique importante pour les problèmes de concours
De nombreux problèmes de probabilités font appel à la reconnaissance des lois discrètes du
programme.
Pour traiter ce type de question il convient, même si l’énoncé ne le demande pas
explicitement de commencer par considérer que l’événement dont on connaît la
probabilité (notée en général p) est un succès. En conséquence de quoi l’événement
contraire constitue un échec. Le succès sera noté [Xi=1] et l’échec sera noté [Xi=0]
On a ainsi défini une variable aléatoire Xi de Bernoulli qui peut prendre 2 valeurs : 0 et 1. On
note alors Xi(  ) = 0;1 ; P[Xi=1] = p et P[Xi=0]=1-p=q
a. Propriétés de la loi de Bernoulli.
On peut s’assurer que Xi définit bien une variable discrète en vérifiant que
En effet :
 P[ Xi  k ] = P[Xi=0]+P[Xi=1]=p+1-p = 1
 P[ Xi  k ] =1
k X (  )
k X (  )
E(Xi) =
 kP[ Xi  k ] = 0.P[Xi=0]+1.P[Xi=1]=0p+1.p=p
k X (  )
E(Xi2)=
k
2
P[ Xi  k ] =02.P[Xi=0]+12.P[Xi=1]=0p+12.p=p
k X (  )
V(Xi)= E(Xi2)-[ E(Xi)]2= p-p2==p(1-p).
La loi de Bernoulli peut donc se définir à l’aide d’un seul paramètre, p, qui est son espérance
mathématique. La variance s’obtient directement à partir de p. On écrit alors :
 X ()  0;1
 P[ X  1]  p

X  B(p)   P[ X  0]  q  1  p
E ( X )  p

V ( X )  pq
b) Reconnaissance d’une loi binômiale
On considère la succession de n essais identiques et indépendants les uns des autres d’une
même épreuve ayant deux issues possibles : le succès avec la probabilité p et l’échec avec la
probabilité q=1-p. On définit une variable X égale au nombre de succès obtenus à l’issue de
ces n épreuves.
X correspond à la succession (ou à la somme) de n épreuves de Bernoulli (puisque leur
caractéristique est d’avoir deux issues possibles : le succès et l’échec) identiques et
indépendantes.
On dit alors que X suit une loi Binômiale définie par 2 paramètres : n = nombre d’épreuves
(de Bernoulli identiques et indépendantes) et p = probabilité du succès pour chaque épreuve.
On écrit :
 X ()  0; nxN

k k nk
 P[ X  k ]  C n p q
X  B(n, p)  
 E ( X )  np
V ( X )  npq
Cette situation se rencontre lorsque l’on considère une urne comportant des boules de deux
couleurs différentes et que l’on cherche la loi du nombre de boules d ‘une des deux couleurs à
l’ssue de n tirages (d’une boule à chaque tirage) avec remise.
En effet, les tirages sont identiques si l’on suppose que l’on prélève toujours une boule à
chaque tirage. En outre, si la boule tirée est systématiquement remise dans l’urne, la
composition de l’urne est constante. Dès lors, la probabilité d’obtenir une boule d’une couleur
donnée est la même à chaque tirage. Les tirages sont donc indépendants les uns des autres.
Remarque importante :
Le modèle d’urne qui vient d’être donné est seulement une illustration. Les énoncés de
problèmes de concours ne portent pas toujours sur des tirages de boules dans des urnes. Il
convient donc de retenir que la loi Binômiale est d’abord la loi du nombre de succès dans une
succession de n épreuves identiques et indépendantes.
Exemple
On considère une entreprise de service après-vente (SAV) qui intervient avec retard avec une
probabilité égale à 0,25. Un client a appelé à 8 dates différentes.
1°) Préciser la loi de X, son espérance et sa variance
2°) Calculer la probabilité que ce client soit victime d’au moins un retard
3°) Calculer la probabilité que ce client soit victime d’au moins 4 retards sachant qu’il en a
subi au moins un.
(ESCAE 82 M2)
1°) Appelons succès l’événement dont on connaît la probabilité, à savoir « intervenir avec
retard » et notons le [Xi=1] ; appelons échec l’événement contraire (à savoir « intervenir
ponctuellement ») et notons le [Xi=0]. On a :
P[Xi=1]=0,25 et P[Xi=0]=1-0,25=0,75, avec Xi(  ) = 0;1
A l’issue de chaque appel, la probabilité d’intervention avec retard est la même. Les appels
peuvent donc être supposés indépendants les uns des autres. Par conséquent, X est la
succession de 8 épreuves de Bernoulli identiques et indépendantes. X suit donc une loi
binômiale :
 X ()  0;8xN

k
k
nk
P[ X  k ]  C8 0,25 0,75
X  B(8, 0,25)  
E ( X )  8 x0,25  2
V ( X )  8 x0,25 x0,75  1,5
2°) P[X  1]=P[(X=1)ou(X=2)ou…ou(X=8)]= P[(X=1)  (X=2)  …  (X=8)]
= P[X=1]+P[X=2]+…+P[X=8] . Ce calcul peut être effectué en posant successivemnt k=1,
k=2,…,k=8. Il est toutefois plus simple de remarquer que, dans la mesure où [X  1] est
l’événement contraire de [X<1] :
P[X  1]=1-P[X<1] =1-P[X=0]=1- C80 0,25 0 0,7580 =1-0,758 =
P[ X  4  1] P[1  X  4]
=
P[ X  1]
P[ X  1]
P[X  1] a été calculé à la question précédente. Il reste donc à calculer :
3°) P[X  4/X  1]=
P[1  X  4 ]= P[X=1]+ P[X=2]+ P[X=3]+ P[X=4]
= C81 0,2510,7581 + C82 0,25 2 0,75 8 2 + C83 0,253 0,7583  C84 0,25 4 0,75 8 4
Conclusion : P[X  4/X  1] =
c) Reconnaissance d’une loi hypergéométrique
On effectue n tirages SANS REMISE dans une population (ou dans une urne) de taille N. On
recherche alors la loi du nombre de réalisations d’un événement dont la probabilité de
réalisation, avant que ne commencent les tirages, est égale à p.
NB : la composition de la population (ou de l’ urne) change à l’issue de chaque tirage puisque
l’individu (ou la boule) qui vient d’être tiré(e) n’est pas remis(e) dans la population (ou das
l’urne).
Soit X le nombre de succès, ou de réalisation de l’événement dont on connaît la probabilité
avant que ne commencent les tirages.
X définit une loi hypergéotrique de paramètres N, n et p :
 X ()  max( 0; n  Nq); min( n; NpxN

k
nk
 P[ X  k ]  C Np C Nq

C Nn
X  H(N, n, p)  
 E ( X )  np

N n
V ( X )  npq
N 1

Remarque importante
Cette loi de tirages sans remise est également la loi des sondages : en effet, si l’on interroge n
personnes issues d’une population globale de taille N, chaque individu est interrogé une seule
fois. En d’autres termes, il n’est pas remis dans la population initiale après avoir été sondé.
Suite de l’exemple précédent
On consière 8 clients différents. On en contacte 4.
On admet qu’un client est mécontent s’il a fait l’objet d’une intervention avec retard.
On note M le nombre de mécontents .
Donner la loi de M, son espérance et sa variance.
M correspond, dans le cadre d’un sondage, au tirage de 4 clients dans une population de 8
clients sans remise : on peut en effet penser que la personne chargée de l’étude de satisfaction
n’interroge chaque client qu’une seule fois.
En outre, avant de commencer les tirages des individus, on sait que la probabilité
d’intervention avec retard, donc de mécontentement est de 0,25, doù :
X  H(8, 4, 0,25)

 X ()  max( 0;4  8 x0,75); min( 4;8 x0,25xN

k
4k
 P[ X  k ]  C8 x 0, 25C8 x 0, 75

C84

 E ( X )  4 x0,25

84
V ( X )  4 x0,25 x0,75
8 1


 X ()  0;2xN

k
4k
 P[ X  k ]  C 2 C 6

C84

E ( X )  1

4
V ( X )  0,75
7

d) Reconnaissance d’une loi géométrique
On effectue n épreuves (de Bernoulli) identiques et indépendantes dont la probabilité de
succès est p pour chacune d’elles. La probabilité de l’échec pour chacune d’elles est notée
q=1-p.
On appelle X le rang du 1er succès. Dès lors :
P[X=k] signifie « probabilité que le 1er succès soit obtenu à l’issue de la k-ième épreuve. En
d’autres termes, les k-1 premières épreuves se sont soldées par des échecs et la k-ième par un
succès.
Soit Ei= « obtention d’un échec à l’issue de la i-ième épreuve » et Si =« obtention d’un succès
à l’issue de la i-ième épreuve ». Dès lors :
P[X=k] = P(E1  E2  ...  Ek-1  Sk).
Comme les épreuves sont supposées indépendantes :
P[X=k] = P(E1)P(E2)...P(Ek-1)P(Sk) = q.q....q p = qk-1p.

k 1 fois
NB : il faut au moins réaliser une épreuve pour obtenir un succès. En outre, il faudra
éventuellement un nombre infini d’épreuves pour obtenir un succès, d’où :
X ()  1;

k 1
 P[ X  k ]  q p

X  G ( p)  E ( X )  1 / p
V ( X )  q / p 2

Suite de l’exemple précédent
Soit Y la loi du rang du 1er retard. Préciser la loi de Y , son espérance et sa variance
Les appels qui définissent une loi de Bernoulli étant identiques et indépendants, le temps
d’attente du 1er retard définit une loi géométrique de même paramètre que la loi de Bernoulli
précédemment évoquée :
X ()  1;

k 1
 P[ X  k ]  0,75 0,25

Y  G (0,25)   E ( X )  1 / 0,25  4
V ( X )  0,75 / 0,25 2

e) Loi de Poisson
La loi de Poisson résulte de la convergence de la loi binômiale. En d’autres termes, lorsque n
est très grand (n  30) et sous réserve que 2 autres conditions soient également satisfaites
(p  0,1 et np<15), on peut remplacer la loi binômiale B(n ; p) par une loi de poisson de
paramètre  avec  =np. On a alors :
 X ()  N

k

X  P( )   P[ X  k ]  e  .
k!

 E ( X )  V ( X )  
Exemple
X suit une loi de Poisson de paramètre 4.
1°) Calculer P[X=5]
2°) Préciser E(X) et V(X)
3°) On démontre que si X et Y sont deux variables indépendantes avec X  P ( ) et
Y  P(  ) alors X+Y  P (   ) . En déduire la variance de X+Y
(D’après ESCAE 85 M2)
45
5!
2°) E(X)=V(X)=4 (la moyenne et la variance sont égales au paramètre de la loi de Poisson)
3°) Pour la raison qui vient d’être évoquée : V(X+Y)= paramètre de la loi de X+Y soit   
1°) P[X=5] = e-4.
RETOUR EN HAUT
RETOUR AU MENU VARIABLES DISCRETES
RETOUR ACCUEIL