chapitre-1-s2-cristallo

Semestre 2 -PCSI PSI
Chapitre 1: Le solide cristallin
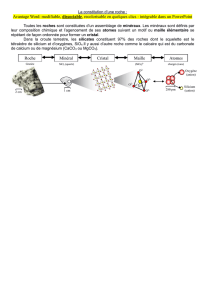
L'étude des cristaux que l'on peut rencontrer dans la nature (pierres précieuses, sel, sucre, neige...)est
appelée cristallographie. La cristallographie a fait beaucoup de progrès au début du 20ème siècle avec la
découverte de la diffraction des rayons X par Max Von Laue (prix Nobel 1914).
Souvenez-vous, en début d'année, nous avions vu que au sein de l'état solide, deux groupes peuvent être
distingués : les solides amorphes et les solides cristallisés (si si je vous jure, on l'a fait!).
Alors que les solides amorphes peuvent prendre une forme quelconque, les solides cristallisés se présentent
sous la forme d'une structure polyédrique, forme géométrique limité par des surfaces planes. Très abondant
dans la nature, l'état cristallin se présente sous forme d'objets de formes et de dimensions très variables. Le
type le plus fréquent est la forme polycristalline constituée par des cristaux de petite taille (inférieur au
millimètre) assemblés de manière compacte et désordonnée. Malgré cette apparence désordonnée, la notion
de cristal reste valable pour décrire ces structures puisque chaque petit cristal est composé d'un très grand
nombre (supérieur à 1018) d'atomes de manière régulière.
I- Notion de base de cristallographie :
1- Le cristal parfait :
Comme le gaz parfait est le modèle idéal de la matière à l'état gazeux, le cristal parfait constitué la base de
l'étude de la matière à l'état solide cristallisé.
Un cristal parfait est constitué d'un arrangement périodique d'entités (atomes, ions, molécules) selon
les trois directions de l'espace. Il est sans défaut et de dimension infinie.
a- Le motif
Le motif est un atome (ou un groupe d'atomes, un ion ou des ions) qui permet de retrouver le cristal pr
pavage régulier dans l'espace.
→ Identifier les motifs dans les deux arrangements présentés.
b- Le réseau
La notion de réseau caractérise la façon dont s'agencent les motifs dans l'espace pour définir le cristal.
En effet la périodicité du dispositif dans les trois directions de l'espace est liée à trois vecteurs de base :
⃗a
,
⃗
b
et
⃗c
, non coplanaires et non colinéaires.
Soient m, n et p des entiers relatifs, soit
⃗
t
le vecteur défini par :
⃗
t=m⃗a+n⃗ b+p⃗c
. A partir d'une
translation de vecteur
⃗
t
appliqué à un point d'origine O on obtient un autre point, puis en faisant varier
les valeurs de m, n, p on obtient une infinité de points. Ces points sont appelés nœuds du réseau.
Pour aller plus loin (Hors programme) : les différents types de réseaux, peuvent être classer selon leurs
propriétés topologiques et de symétries. On obtient ainsi 14 types de réseaux, dit réseaux de Bravais. (Voir
annexe)
→ Placer les vecteur de base sur les réseaux ci-dessous.
1

→ Quelle(s) particularité(s) présentent ces vecteurs de bases dans chaque situation ?
→ Quelle serait la classification du réseau 2 dans la classification de Bravais donné en Annexe.
→ Repérer ce que l'on appelle un nœud du réseau.
c- Maille
On observe que dans l'exemple du réseau cubique,
le réseau peut-être décrit comme l'assemblage de
cubes identiques comportant chacun un certain
nombre de motifs. Dans un cas plus général, les
vecteurs
⃗a
,
⃗
b
et
⃗c
ne définissent pas un
cube mais un parallélépipède.
Le cristal parfait est un assemblage de
parallélépipède identiques, appelés mailles,
comportant chacun le même nombre de motifs.
2- Construction des assemblages compacts :
Parmi les 14 réseaux de Bravais, trois ont une importance particulière : ce sont les structures les plus
compactes. Ces structures sont particulièrement adaptées pour étudier les métaux, et dans une moindre
mesure les solides ioniques et covalents. On assimile les atomes à des sphères dures.
Il n'existe qu'un mode d'assemblage compact (→ minimiser les espaces vides dans la structure) pour
construire un plan (plan A), tout comme il n'existe qu'une seule manière d'empiler deux plans de manière
compacte (empilement des plans A et B).
Dès lors que nous voulons ajouter un troisième plan pour construire le cristal, possibilités s'offrent à nous :
2
Réseau cubique Réseau 2
Plan compact A
Empilement compact de
deux plans (plan A en traits
pleins, plan B en pointillés)

•Empilement A-B-A : On peut superposer le troisième plan au plan A :
•Empilement de type A-B-C : le troisième plan n'est pas superposé aux deux autres plans.
3- Description et étude d'une maille : la maille cubique faces centrées :
Nous verrons ici les définitions essentielles pour l'étude d'une maille. Pour chaque paramètre défini, il faut
trouver sa valeur pour la maille cubique faces centrées (à connaître absolument et à savoir redémontrer).
On note a, le paramètre de maille, a représente l'arrête du cube de la maille c.f.c. et R le rayon d'un
atome.
(Il faut également savoir appliquer ces concepts à d'autres mailles, dont on vous donnerait le schéma, nous
ferons d'autres exemples dans la suite du cours.)
Population (ou Appartenance) : notée N (ou A) : c'est le nombre de motifs appartenant en propre à la
maille.
Coordinence : La coordinence d'un atome ou d'un ion au sein d'une structure cristalline est le nombre de
plus proches voisins que possède cet atome ou cet ion.
Compacité : La compacité C d'un solide est la fraction de volume occupée par la matière en considérant les
atomes et les ions comme des sphères dures.
C=volume occupé par la population de la maille
volume de la maille
Masse volumique :
ρ=masse de la population de la maille
volume de la maille
Exemple : l'argent pur cristallise dans un structure de type CFC. Sa masse molaire est de 107,9g.mol-1 et son
3
Structure
hexagonale
compacte
(h.c)
Pour étudier cette structure, il
est plus astucieux de regarder la
maille de biais, afin d'obtenir
une structure cubique.
L'empilement des plans A-B-C
se fait donc selon la diagonale
du cube.
c

paramètre de maille vaut a=407pm. On rappelle que le nombre d'Avogadro vaut Na = 6,02.1023mol-1.
→ Déterminer la masse volumique de l'argent.
Pour réinvestir : Etude de la maille hexagonale compacte.
1- Déterminer la population et la compacité pour la maille hexagonale compacte.
2- Déterminer la masse volumique du titane sachant qu'il cristallise dans la structure h.c avec les paramètres
de maille suivant : a = 295,1pm, c=469,2pm. M(Ti) = 47,88g.mol-1.
II- Les solides métalliques :
1- La formation des alliages :
Les alliages sont des combinaisons d'un métal avec d'autres éléments chimiques. Le terme « alliage »
est parfois remplacé par le terme « solution solide ».
Il existe des alliages de substitution, comme par exemple l'alliage cuivre-or, ou des alliages d'insertion,
comme par exemple l'acier (alliage carbone-fer).
a- Qu'est ce qui distingue un alliage d'insertion d'un alliage de substitution ? Proposer un schéma.
b- A quelle(s) condition(s) sur la taille des atomes et des « sites vides » peut-on avoir un alliage d'insertion ?
de substitution ?
2- Sites interstitiels :
Comme le montre la compacité de la maille cfc, même les structures compactes présentent des sites
inoccupés (environ 25% de l'espace). On nomme ces sites : sites interstitiels.
Il existe deux types d'interstices entre atomes dans la structure c.f.c : les sites octaédriques et tétraédriques.
Un site octaédrique (en abrégé, site O) est un interstice entre six atomes positionnées aux sommets d'un
octaèdre. Un site tétraédrique (en abrégé, site T) est un interstice entre quatre atomes positionnées aux
sommets d'un tétraèdre.
On appelle le rayon d'habilité d'un site interstitiel, le rayon de la plus grande sphère que l'on peut placer
dans cette cavité.
a- Pour la structure c.f.c : Localiser les sites octaédriques et tétraédriques. Dénombrer le nombre de site par
maille (population) et déterminer l'expression du rayon d'habilité du site en fonction du rayon R des atomes
constituants la maille.
b- Sachant que l'or cristallise selon une structure cfc de paramètre de maille aAu=408pm, montrer qu'il ne
peut faire avec le cuivre (RCu =128pm) qu'un alliage de substitution.
c- Le rayon atomique du carbone est de 70pm tandis que celui du fer est de 140pm. Sachant que le fer
cristallise selon une maille cfc, montrer que l'acier est un alliage d'insertion. Préciser dans quelles cavités les
4

atomes de carbone se logent.
Pour information : les sites interstitiels dans la maille hexagonale compacte (le décompte a été fait pour la
maille triple, il y a donc en réalité 2 sites O et 4 sites T par maille hc.)
3- Quelques propriétés des métaux :
La liaison métallique existant entre les atomes au sein du métal et assurant la cohésion du cristal a une
énergie assez grande, de l'ordre de 100 à 500kJ.mol-1 et sont non directionnelles. Pour expliquer les
propriétés physiques des cristaux métalliques, plusieurs modèles de liaison métalliques ont été développés.
Dans le modèle du gaz d'électrons, on considère que :
–Les atomes perdent leurs électrons de valence et donnent des cations.
–Ces électrons de valence forment un gaz d'électrons « libres ».
–Le cristal métallique est un assemblage tridimensionnel périodique de ces cations enveloppés par le
gaz d'électrons libres.
a- Rappeler où se trouvent les métaux dans la classification périodique. Justifier la phrase : « Les atomes
perdent leurs électrons de valence et donnent des cations. »
b- Comment peut-on justifier la résistance des métaux face à une déformation ?
c- Comment peut-on justifier la malléabilité (aptitude à la déformation sans rupture) des métaux ?
d- Comment justifier que la masse volumique des métaux soit généralement élevée ?
e- L'examen du fer montre qu'il n'est pas mécaniquement très performant, il est peu résistant. Ce constat est
souvent valable pour la plupart des métaux purs. L'acier est par contre lui beaucoup plus résistant, comment
peut-on expliquer cela ?
Remarque : Les alliages sont particulièrement intéressant, car ils présentent des propriétés différentes tant au
niveau de la dureté, de la résistance à la corrosion ou encore au niveau des propriétés électriques.
III- Les solides covalents :
Autour du carbone : La carbone est présent dans des milliers de composés de la vie, c'est pourquoi on lui a
consacré une branche à part entière de la chimie : la chimie organique. Par contre, à l'état de corps purs,
on peut le trouver sous diverses formes, on parle alors de formes allotropiques. Ceci comprend le graphite,
le diamant, le fullerène, le nanotube et le graphène!
https://prezi.com/qfmjmjovrljq/les-formes-allotropiques-du-carbone/
1- Etude du diamant
(Document en page suivant)
1- La maille diamant peut-elle être compacte comme l'est la maille cfc parfaite?
2- Que pouvez-vous dire de la géométrie autour de chaque atome de carbone dans la maille ? Cela
5